Question
Question: Two identical bricks of length L are piled one on top of the other on a table as shown in the figure...
Two identical bricks of length L are piled one on top of the other on a table as shown in the figure. The maximum distance S the top brick can overhang the table with the system still balanced is:
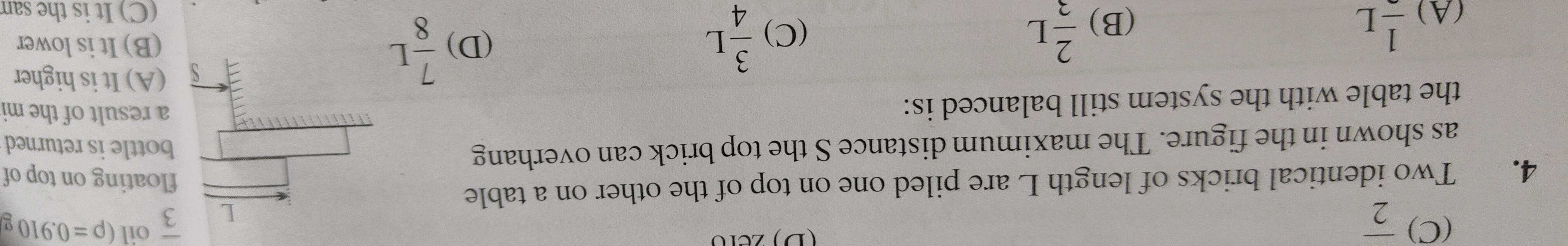
21L
23L
43L
87L
$\frac{3}{4}L
Solution
To find the maximum distance S the top brick can overhang the table while the system remains balanced, we need to ensure that the center of mass (CM) of each part of the system is supported by the part below it. We work from top to bottom.
Let L be the length of each identical brick and m be the mass of each brick. The center of mass of a uniform brick is at its geometric center, i.e., L/2 from either end.
Step 1: Stability of the top brick (Brick 1) relative to the bottom brick (Brick 2).
For the top brick to be stable on the bottom brick, its center of mass must lie over the supporting area of the bottom brick. To achieve the maximum possible overhang, the center of mass of the top brick must be exactly at the rightmost edge of the bottom brick.
If the top brick's CM is at the right edge of the bottom brick, and its CM is L/2 from its own right end, then the top brick overhangs the bottom brick by a distance L/2.
Let x_1 be the overhang of the top brick over the bottom brick.
Maximum x_1 = L/2.
Step 2: Stability of the combined system (Brick 1 + Brick 2) relative to the table.
Now, consider the system of the two bricks. For this combined system to be stable on the table, its overall center of mass must lie over the supporting area of the table. To maximize the total overhang S of the top brick over the table, the combined center of mass of the two bricks must be exactly at the rightmost edge of the table.
Let's set up a coordinate system with the rightmost edge of the table as the origin (x = 0).
Let x_2 be the overhang of the bottom brick over the table. This means the rightmost end of the bottom brick (Brick 2) is at coordinate x = x_2.
- Position of CM of Brick 2: Since the bottom brick has length
L, its center of mass isL/2to the left of its right end. So, the coordinate of the CM of Brick 2 isx_{CM2} = x_2 - L/2. - Position of CM of Brick 1: From Step 1, the CM of the top brick (Brick 1) is at the rightmost edge of the bottom brick (Brick 2). So, the coordinate of the CM of Brick 1 is
x_{CM1} = x_2.
The combined center of mass of the two-brick system (x_{CM_system}) is given by:
xCMsystem=m+mm⋅xCM1+m⋅xCM2
xCMsystem=2mm(x2)+m(x2−L/2)
xCMsystem=2x2+x2−L/2
xCMsystem=22x2−L/2
For maximum overhang, the combined CM must be at the table edge (x_{CM_system} = 0):
22x2−L/2=0
2x2−L/2=0
2x2=L/2
x2=4L
This means the bottom brick overhangs the table by L/4.
Step 3: Calculate the total overhang S.
The question asks for the maximum distance S the top brick can overhang the table. This is the coordinate of the rightmost end of the top brick relative to the table edge.
The rightmost end of the top brick is L/2 to the right of its center of mass (x_{CM1}).
So, the coordinate of the rightmost end of the top brick is x_{CM1} + L/2.
Since x_{CM1} = x_2, the total overhang S is:
S=x2+2L
Substitute the value of x_2 = L/4:
S=4L+2L
S=4L+42L
S=43L
Thus, the maximum distance S the top brick can overhang the table is 3L/4.
