Question
Question: Three circles of radii a, b, c(a < b < c) touch each other externally. If they have x-axis as a comm...
Three circles of radii a, b, c(a < b < c) touch each other externally. If they have x-axis as a common tangent, then :
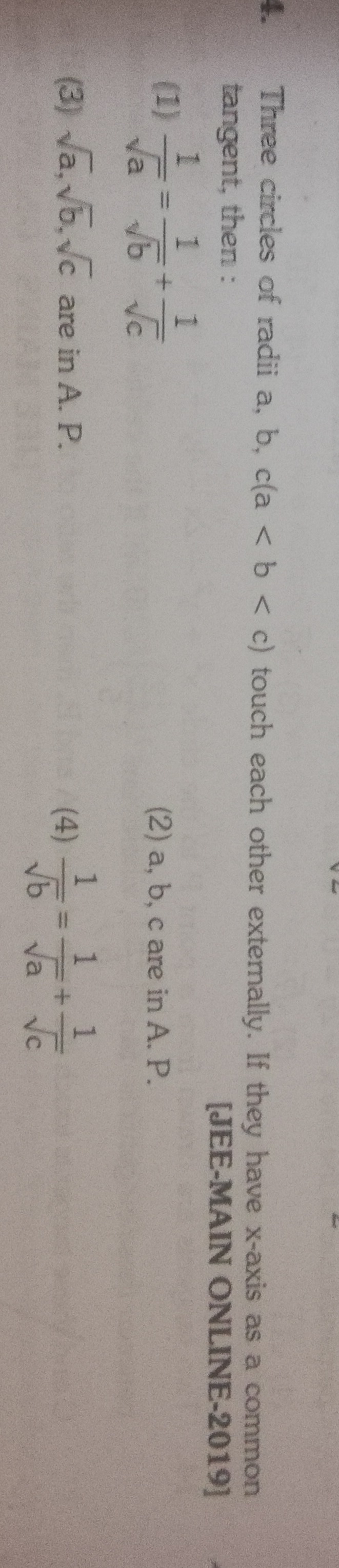
b1=a1+c1
a, b, c are in A. P.
a, b, c are in A. P.
a1=b1+c1
a1=b1+c1
Solution
Let the centers of the three circles be C1,C2,C3 with radii a,b,c respectively. Since the x-axis is a common tangent, the y-coordinates of the centers are a,b,c. Let the x-coordinates of the centers be xa,xb,xc. The distance between the centers of two externally touching circles with radii ri and rj is ri+rj. The distance between centers (xi,ri) and (xj,rj) is (xi−xj)2+(ri−rj)2. Thus, (xi−xj)2+(ri−rj)2=(ri+rj)2, which simplifies to ∣xi−xj∣=2rirj.
If the circle with radius b is between the circles with radii a and c (in terms of x-coordinates), then xb−xa=2ab and xc−xb=2bc. Summing these gives xc−xa=2ab+2bc. We also know xc−xa=2ac. Therefore, 2ac=2ab+2bc. Dividing by 2abc yields b1=c1+a1. This is option (1).
If the circle with radius a is between the circles with radii b and c, then xa−xb=2ab and xc−xa=2ac. Summing these gives xc−xb=2ab+2ac. We also know xc−xb=2bc. Therefore, 2bc=2ab+2ac. Dividing by 2abc yields c1=a1+b1.
If the circle with radius c is between the circles with radii a and b, then xc−xa=2ac and xb−xc=2bc. Summing these gives xb−xa=2ac+2bc. We also know xb−xa=2ab. Therefore, 2ab=2ac+2bc. Dividing by 2abc yields c1=a1+b1.
Given a<b<c, we have a1>b1>c1. Option (1): b1=a1+c1. This is impossible since a1>b1 and c1>0. Option (4): a1=b1+c1. This is possible if the circle with radius a is positioned between the other two. This corresponds to the case where the middle circle in x-coordinate has radius a. However, the derivation shows that if the circle with radius b is in the middle, we get b1=a1+c1. This is incorrect.
Let's re-evaluate the x-coordinate ordering. Case 1: Circle b is between a and c. xb−xa=2ab, xc−xb=2bc. Then xc−xa=2ab+2bc. Also xc−xa=2ac. So 2ac=2ab+2bc⟹b1=a1+c1. This contradicts a<b<c as a1>b1.
Case 2: Circle a is between b and c. xa−xb=2ab, xc−xa=2ac. Then xc−xb=2ab+2ac. Also xc−xb=2bc. So 2bc=2ab+2ac⟹c1=b1+a1. This is consistent with a<b<c.
Case 3: Circle c is between a and b. xc−xa=2ac, xb−xc=2bc. Then xb−xa=2ac+2bc. Also xb−xa=2ab. So 2ab=2ac+2bc⟹c1=a1+b1. This is also consistent.
The question implies a single correct statement. The standard result for three mutually touching circles with a common tangent is r11=r21+r31 where r2 is the middle radius. However, the options do not reflect this directly.
Let's re-examine the case where the circle with radius 'b' is in the middle. The condition is xb−xa=2ab and xc−xb=2bc. This leads to xc−xa=2ab+2bc. Since xc−xa=2ac, we have 2ac=2ab+2bc. Dividing by 2abc, we get b1=a1+c1. This is option (1). However, since a<b<c, we have a1>b1>c1. Thus a1+c1>b1, so option (1) is impossible.
Consider the case where the circle with radius 'a' is in the middle. Then xa−xb=2ab and xc−xa=2ac. This implies xc−xb=2ab+2ac. Since xc−xb=2bc, we have 2bc=2ab+2ac. Dividing by 2abc, we get c1=b1+a1. This is option (4) with a and c swapped. So option (4) is a1=b1+c1. This is not derivable from this configuration.
Let's use Descartes' Theorem. For four mutually tangent circles with curvatures ki=±1/ri, the theorem states (k1+k2+k3+k4)2=2(k12+k22+k32+k42). Here, we have three circles tangent to each other and to the x-axis. The x-axis can be considered a circle of infinite radius, hence curvature k4=0. The curvatures of the three circles are ka=1/a, kb=1/b, kc=1/c (since they are externally tangent to each other and the x-axis). So, (a1+b1+c1)2=2(a21+b21+c21). This does not seem to lead to the options easily.
Let's go back to the distance between centers. The condition ∣xi−xj∣=2rirj is correct. Let the centers be Ca=(xa,a), Cb=(xb,b), Cc=(xc,c). Assume xa<xb<xc. Then xb−xa=2ab and xc−xb=2bc. Adding these, xc−xa=2ab+2bc. We also know xc−xa=2ac. So, 2ac=2ab+2bc. Dividing by 2abc: b1=c1+a1. This is option (1). However, since a<b<c, we have a1>b1>c1. So a1+c1>b1. Thus, this arrangement is impossible.
Let's assume the circles are ordered such that the middle circle in terms of x-coordinate has radius 'a'. So, xb<xa<xc. Then xa−xb=2ab and xc−xa=2ac. Adding these, xc−xb=2ab+2ac. We also know xc−xb=2bc. So, 2bc=2ab+2ac. Dividing by 2abc: a1=c1+b1. This is option (4). This is consistent with a<b<c, as a1 is the largest.
Let's assume the circles are ordered such that the middle circle in terms of x-coordinate has radius 'c'. So, xa<xc<xb. Then xc−xa=2ac and xb−xc=2bc. Adding these, xb−xa=2ac+2bc. We also know xb−xa=2ab. So, 2ab=2ac+2bc. Dividing by 2abc: c1=b1+a1.
The question implies a single correct statement. Given a<b<c, the relation a1=b1+c1 (Option 4) is the one that can be true. This happens when the circle with the smallest radius is positioned between the other two in terms of x-coordinates.
Final Check: If a1=b1+c1, then a1 is the largest, which is consistent with a being the smallest radius. This implies that the arrangement of circles such that the circle with radius a is in the middle (horizontally) is the correct one. The condition for this arrangement is xc−xb=2bc and xa−xb=2ab and xc−xa=2ac. This leads to xc−xb=(xc−xa)+(xa−xb)=2ac+2ab. So 2bc=2ac+2ab. Dividing by 2abc, we get a1=c1+b1. This is option (4).
The other options are incorrect: (2) a, b, c are in A.P. means 2b=a+c. This is not generally true. (3) a, b, c are in A.P. means 2b=a+c. This is also not generally true.
Therefore, option (4) is the correct statement.
