Question
Question: The value of $\csc^2 \frac{2\pi}{7} + \csc^2 \frac{2\pi}{7} + \csc^2 \frac{4\pi}{7}$ is equal to 8...
The value of csc272π+csc272π+csc274π is equal to 8
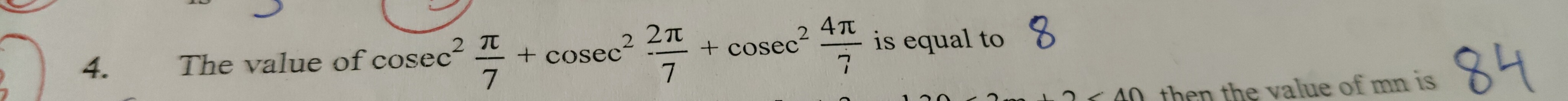
False
Solution
The question asks to verify if the statement "The value of csc272π+csc272π+csc274π is equal to 8" is true or false. The expression can be simplified as 2csc272π+csc274π.
We use the identity csc2x=1+cot2x. So, the expression becomes: 2csc272π+csc274π=2(1+cot272π)+(1+cot274π) =2+2cot272π+1+cot274π =3+2cot272π+cot274π
We know that cot(π−x)=−cotx, which implies cot2(π−x)=cot2x. Therefore, cot274π=cot2(π−73π)=cot273π. Substituting this into the expression: 3+2cot272π+cot273π
Now, we use a standard identity for the sum of squares of cotangents: For an odd integer n, the sum of squares of cotangents is given by: ∑k=1(n−1)/2cot2nkπ=6(n−1)(n−2) For n=7, (n−1)/2=(7−1)/2=3. So, for n=7: cot27π+cot272π+cot273π=6(7−1)(7−2)=66×5=5
Let the given expression be E. We are checking if E=8. So, we need to check if 3+2cot272π+cot273π=8. This implies 2cot272π+cot273π=5.
From the identity, we know that cot27π+cot272π+cot273π=5. If the statement is true, then it must be that: 2cot272π+cot273π=cot27π+cot272π+cot273π Subtracting cot272π+cot273π from both sides, we get: cot272π=cot27π This implies cot72π=±cot7π. Since both 7π and 72π lie in the interval (0,π/2), their cotangent values are positive. Thus, we must have cot72π=cot7π. However, the cotangent function is strictly decreasing in the interval (0,π/2). Since 7π<72π, it must be that cot7π>cot72π. Therefore, cot27π=cot272π. This contradicts our assumption that the given statement is true.
Hence, the statement "The value of csc272π+csc272π+csc274π is equal to 8" is false.
Note: If the question had been csc27π+csc272π+csc274π, then the value would be: (1+cot27π)+(1+cot272π)+(1+cot274π) =3+cot27π+cot272π+cot273π =3+5=8 This is a common identity, which suggests a possible typo in the original question. However, based on the question as stated, the value is not 8.
