Question

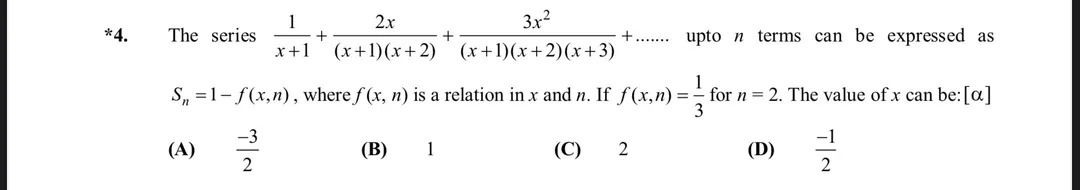
The series $\frac{1}{x+1} + \frac{2x}{(x+1)(x+2)} + \frac{3x^2}{(x+1)(x+2)(x+3)} + ......$ upto $n$ terms can be expressed as $S_n = 1 - f(x,n)$, where $f(x,n)$ is a relation in $x$ and $n$. If $f(x,n) = \frac{1}{3}$ for $n = 2$. The value of $x$ can be: $[\alpha]$

• A. $-\frac{3}{2}$
• B. 1
• C. 2
• D. $-\frac{1}{2}$

Answer 1

Answer: (C), (D)

2 and $-\frac{1}{2}$

Answer 2

Given the series

$$S_n = \frac{1}{x+1} + \frac{2x}{(x+1)(x+2)} + \frac{3x^2}{(x+1)(x+2)(x+3)} + \ldots \text{ (up to $n$ terms)}$$

and we have

$$S_n = 1 - f(x,n).$$

For $n=2$, it's given that $f(x,2)=\frac{1}{3}$. So,

$$S_2 = 1 - \frac{1}{3} = \frac{2}{3}.$$

Now, the first two terms are:

$$T_1 = \frac{1}{x+1}, \quad T_2 = \frac{2x}{(x+1)(x+2)}.$$

Thus,

$$S_2 = \frac{1}{x+1} + \frac{2x}{(x+1)(x+2)} = \frac{2}{3}.$$

Multiply both sides by $(x+1)(x+2)$:

$$(x+2) + 2x = \frac{2}{3}(x+1)(x+2).$$

This simplifies to:

$$3x + 2 = \frac{2}{3}(x^2 + 3x + 2).$$

Multiply both sides by 3:

$$9x + 6 = 2x^2 + 6x + 4.$$

Bring all terms to one side:

$$2x^2 + 6x + 4 - 9x - 6 = 0 \quad \Rightarrow \quad 2x^2 - 3x - 2 = 0.$$

Solving the quadratic:

$$x = \frac{3 \pm \sqrt{(-3)^2 - 4\cdot2\cdot(-2)}}{2\cdot2} = \frac{3 \pm \sqrt{9+16}}{4} = \frac{3 \pm 5}{4}.$$

So,

$$x = \frac{8}{4} = 2 \quad \text{or} \quad x = \frac{-2}{4} = -\frac{1}{2}.$$

Thus, the possible values of $x$ are 2 and $-\frac{1}{2}$.