Question

The normal at a variable point P on an ellipse E of eccentricity $e=\frac{2}{3}$ meets the axes of the ellipse in Q and R then find the eccentric of locus of the mid-point of QR.

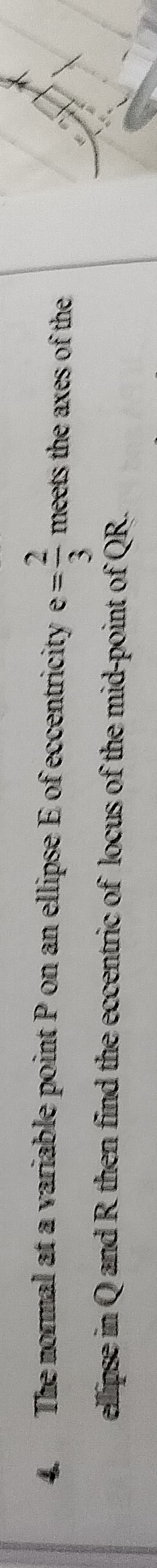
• A. 2/3
• B. 3/2
• C. 4/9
• D. 9/4

Answer 1

Answer: (A)

2/3

Answer 2

Let the ellipse be $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$. The eccentricity is $e = \frac{2}{3}$. The equation of the normal at $P(a \cos \theta, b \sin \theta)$ is $\frac{ax}{\cos \theta} - \frac{by}{\sin \theta} = a^2 - b^2 = a^2e^2$.

The normal meets the x-axis at $Q(ae^2 \cos \theta, 0)$ and the y-axis at $R(0, -\frac{a^2e^2}{b} \sin \theta)$.

Let $M(X, Y)$ be the midpoint of QR. $X = \frac{ae^2}{2} \cos \theta \implies \cos \theta = \frac{2X}{ae^2}$ $Y = -\frac{a^2e^2}{2b} \sin \theta \implies \sin \theta = -\frac{2bY}{a^2e^2}$

Using $\cos^2 \theta + \sin^2 \theta = 1$: $(\frac{2X}{ae^2})^2 + (\frac{2bY}{a^2e^2})^2 = 1$ $\frac{4X^2}{a^2e^4} + \frac{4b^2Y^2}{a^4e^4} = 1$ $\frac{X^2}{(a^2e^4/4)} + \frac{Y^2}{(a^4e^4/4b^2)} = 1$

Let the locus be $\frac{X^2}{A^2} + \frac{Y^2}{B^2} = 1$, where $A^2 = \frac{a^2e^4}{4}$ and $B^2 = \frac{a^4e^4}{4b^2} = \frac{a^2e^4}{4(1-e^2)}$. Since $e^2 = 4/9$, $1-e^2 = 5/9$. $A^2 = \frac{a^2(4/9)^2}{4} = \frac{4a^2}{81}$ $B^2 = \frac{a^2(4/9)^2}{4(5/9)} = \frac{4a^2}{45}$

Since $B^2 > A^2$, the major axis is along the Y-axis. The eccentricity $(e')^2$ of the locus is $1 - \frac{A^2}{B^2}$. $(e')^2 = 1 - \frac{4a^2/81}{4a^2/45} = 1 - \frac{45}{81} = 1 - \frac{5}{9} = \frac{4}{9}$. $e' = \sqrt{\frac{4}{9}} = \frac{2}{3}$.