Question

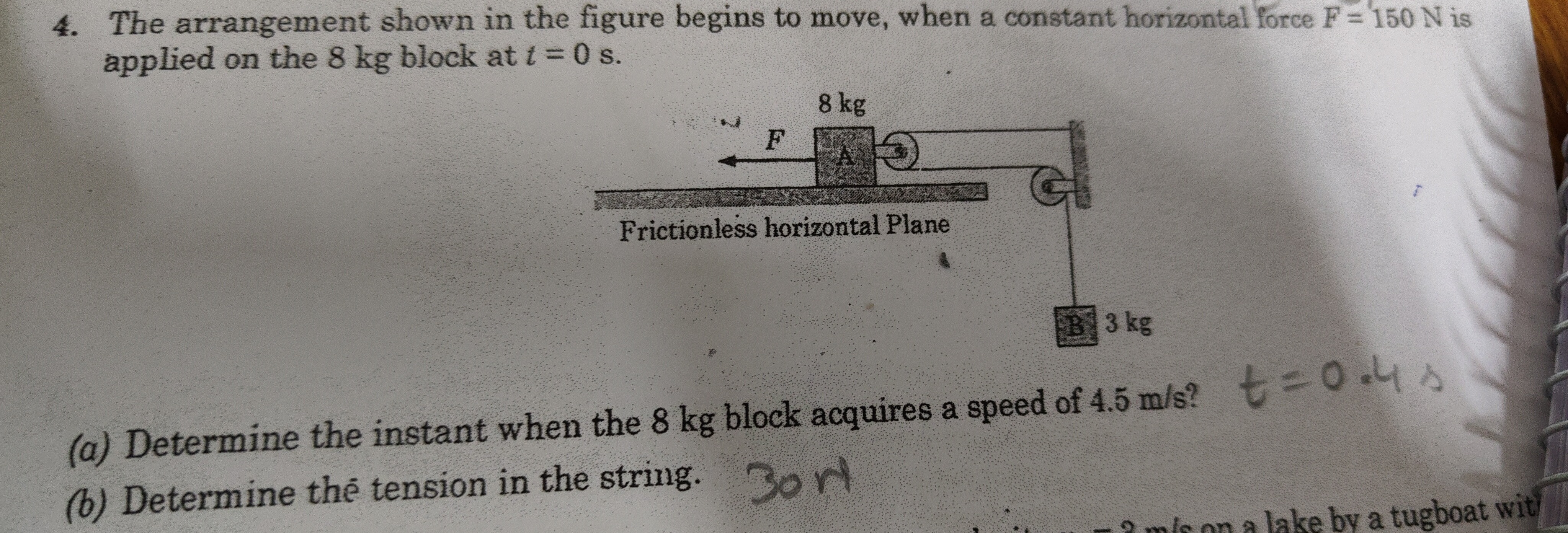
The arrangement shown in the figure begins to move, when a constant horizontal force F = 150 N is applied on the 8 kg block at t = 0 s.

(a) Determine the instant when the 8 kg block acquires a speed of 4.5 m/s?

(b) Determine the tension in the string.

Answer 1

a) 0.4125 s, b) 690/11 N

Answer 2

The problem describes a system consisting of two blocks connected by a string over a pulley. Block A (8 kg) is on a frictionless horizontal plane, and Block B (3 kg) hangs vertically. A constant horizontal force F = 150 N is applied to Block A. We need to find the time for Block A to reach a certain speed and the tension in the string.

1. Define variables and set up Free Body Diagrams (FBDs):

Let $m_A = 8$ kg and $m_B = 3$ kg.
Let the applied force be $F = 150$ N.
Let the acceleration of the system be $a$. Since the string is inextensible and the pulley is ideal, both blocks will have the same magnitude of acceleration.
We will use $g = 10 \text{ m/s}^2$ for acceleration due to gravity, which is a common approximation in such problems unless specified otherwise.

From the diagram, the force F is applied to Block A, pulling it to the left. The string connects Block A (from its right side) to Block B over a pulley.
If Block A moves to the left, then the string must be pulling Block A to the right (opposing the motion or acting as a resistive force). Consequently, Block B must move upwards.

FBD for Block A (8 kg):

• Horizontal forces:
  • Applied force F to the left.
  • Tension T to the right.
• Vertical forces (normal force and weight) balance each other as there is no vertical acceleration on the horizontal plane.

Applying Newton's Second Law ($\Sigma F = ma$) in the horizontal direction, assuming left as positive:
$F - T = m_A a$
$150 - T = 8a$ --- (Equation 1)

FBD for Block B (3 kg):

• Vertical forces:
  • Tension T upwards.
  • Weight $m_B g$ downwards.

Applying Newton's Second Law ($\Sigma F = ma$) in the vertical direction, assuming upward as positive:
$T - m_B g = m_B a$
$T - (3 \text{ kg})(10 \text{ m/s}^2) = 3a$
$T - 30 = 3a$ --- (Equation 2)

2. Solve the system of equations for a and T:

From Equation 2, express T:
$T = 30 + 3a$

Substitute this expression for T into Equation 1:
$150 - (30 + 3a) = 8a$
$150 - 30 - 3a = 8a$
$120 = 8a + 3a$
$120 = 11a$
$a = \frac{120}{11} \text{ m/s}^2$

Now, calculate T using the value of a:
$T = 30 + 3 \left( \frac{120}{11} \right)$
$T = 30 + \frac{360}{11}$
$T = \frac{30 \times 11 + 360}{11}$
$T = \frac{330 + 360}{11}$
$T = \frac{690}{11} \text{ N}$

3. Answer the specific questions:

(a) Determine the instant when the 8 kg block acquires a speed of 4.5 m/s?
The block starts from rest, so initial velocity $u = 0$ m/s.
The final velocity required is $v = 4.5$ m/s.
The acceleration is $a = \frac{120}{11} \text{ m/s}^2$.
Using the kinematic equation $v = u + at$:
$4.5 = 0 + \left( \frac{120}{11} \right) t$
$t = \frac{4.5 \times 11}{120}$
$t = \frac{49.5}{120}$
$t = \frac{99}{240}$ (multiplying numerator and denominator by 2 to remove decimal)
$t = \frac{33}{80}$ seconds (dividing numerator and denominator by 3)
$t = 0.4125$ seconds

(b) Determine the tension in the string.
From our calculation above:
$T = \frac{690}{11} \text{ N}$
$T \approx 62.73 \text{ N}$

The solution is consistent. The acceleration $a = 120/11 \approx 10.91 \text{ m/s}^2$ is positive, meaning Block A moves left and Block B moves up. The tension $T = 690/11 \approx 62.73$ N is positive, as expected. Also, $F=150$ N is greater than $T \approx 62.73$ N, and $T \approx 62.73$ N is greater than $m_B g = 30$ N, which confirms the assumed direction of motion.

Explanation of the solution:

1. Draw Free Body Diagrams (FBDs) for each block, identifying all forces acting on them (applied force, tension, weight, normal force).
2. Based on the direction of the applied force and the pulley setup, deduce the direction of motion for each block and the relationship between their accelerations (they are equal in magnitude).
3. Apply Newton's Second Law ($\Sigma F = ma$) to each block along the direction of motion.
   • For Block A: $F - T = m_A a$ (since F pulls left, T pulls right)
   • For Block B: $T - m_B g = m_B a$ (since Block B moves up)
4. Solve the system of two linear equations for the unknown acceleration ($a$) and tension ($T$).
5. Use the calculated acceleration and kinematic equations ($v = u + at$) to find the time required for Block A to reach the specified speed.

Answer:
(a) The instant when the 8 kg block acquires a speed of 4.5 m/s is 0.4125 s.
(b) The tension in the string is 690/11 N (approximately 62.73 N).