Question

Suppose that a normal drawn at a point P (at 2, 2at) to parabola $y^2 = 4ax$ meets it again at Q. If the length of PQ is minimum, then :

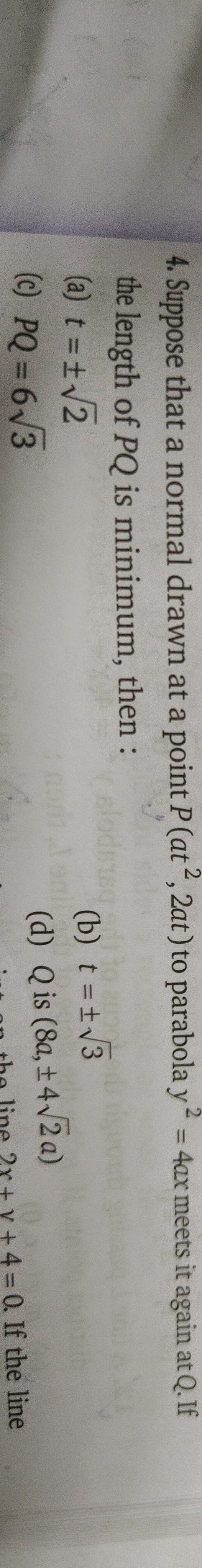
• A. $t = \pm \sqrt{2}$
• B. $t = \pm \sqrt{3}$
• C. $PQ = 6\sqrt{3}$
• D. $Q$ is $(8a, \pm 4\sqrt{2a})$

Answer 1

Answer: (A)

t = \pm \sqrt{2}

Answer 2

The coordinates of point P on the parabola $y^2 = 4ax$ are given by $(at^2, 2at)$. The condition for a normal chord is that if it meets the parabola at $t$, it meets again at $t'$ where $t' = -t - \frac{2}{t}$.

The square of the length of the chord PQ is given by: $PQ^2 = (at'^2 - at^2)^2 + (2at' - 2at)^2$ $PQ^2 = a^2(t'^2 - t^2)^2 + 4a^2(t' - t)^2$ $PQ^2 = a^2(t' - t)^2 [(t' + t)^2 + 4]$

Substituting $t' + t = -\frac{2}{t}$ and $t' - t = -2t - \frac{2}{t} = -2\left(t + \frac{1}{t}\right)$: $PQ^2 = a^2 \left(-2\left(t + \frac{1}{t}\right)\right)^2 \left[\left(-\frac{2}{t}\right)^2 + 4\right]$ $PQ^2 = a^2 \left(4\frac{(t^2+1)^2}{t^2}\right) \left[\frac{4}{t^2} + 4\right]$ $PQ^2 = \frac{16a^2(t^2+1)^3}{t^4}$

To minimize PQ, we minimize $PQ^2$. Let $u = t^2$. Then $PQ^2 = \frac{16a^2(u+1)^3}{u^2}$. Differentiating with respect to $u$ and setting to zero: $\frac{d(PQ^2)}{du} = 16a^2 \frac{(u+1)^2(u-2)}{u^3} = 0$ This implies $u-2 = 0$, so $u=2$. Since $u=t^2$, we have $t^2=2$, which means $t = \pm \sqrt{2}$.

The minimum length of PQ is $6a\sqrt{3}$, which occurs when $t = \pm \sqrt{2}$. The coordinates of Q are $(8a, \mp 4a\sqrt{2})$.

Option (a) states $t = \pm \sqrt{2}$, which is the condition for minimum length. Option (c) states $PQ = 6\sqrt{3}$, which is only true if $a=1$. Option (d) states $Q$ is $(8a, \pm 4\sqrt{2a})$, which is only true if $a=1$. Therefore, the only universally correct statement is (a).