Question

Solve for $x: \sin^{-1}\left(\sin\left(\frac{2x^2+4}{1+x^2}\right)\right)<\pi-3$

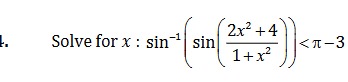
Answer 1

(-1, 1)

Answer 2

Let $y = \frac{2x^2+4}{1+x^2}$. The range of $y$ is $(2, 4]$. For $y \in (2, 4]$, $\sin^{-1}(\sin(y)) = \pi-y$. The inequality becomes $\pi-y < \pi-3$, which simplifies to $y > 3$. Thus, we need $3 < y \le 4$. Substituting back $y = \frac{2x^2+4}{1+x^2}$, we get $3 < \frac{2x^2+4}{1+x^2} \le 4$. The inequality $3 < \frac{2x^2+4}{1+x^2}$ yields $x^2 < 1$, or $-1 < x < 1$. The inequality $\frac{2x^2+4}{1+x^2} \le 4$ is true for all real $x$. The intersection of these conditions is $-1 < x < 1$.