Question

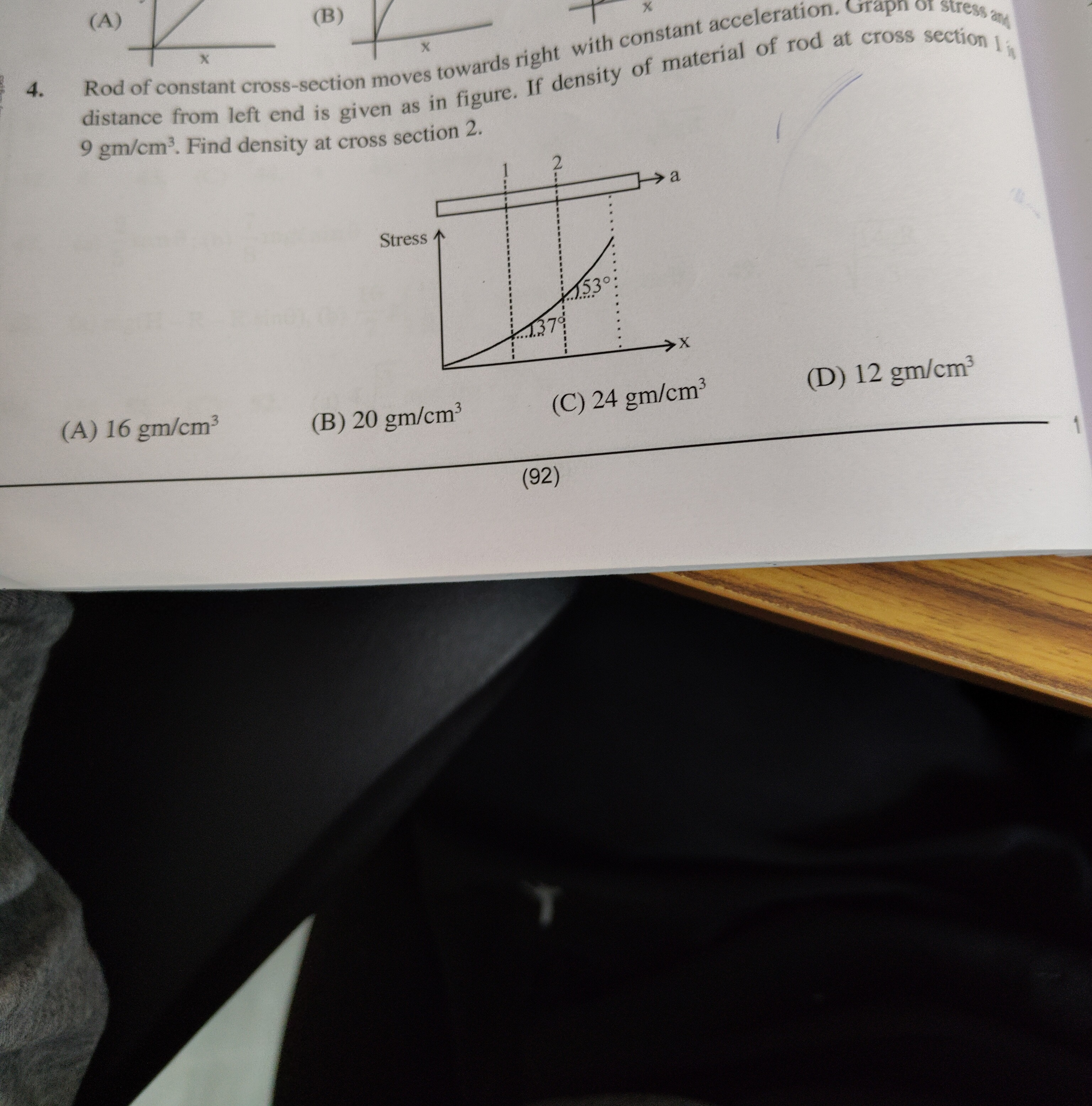
Rod of constant cross-section moves towards right with constant acceleration. Graph of stress and distance from left end is given as in figure. If density of material of rod at cross section 1 is 9 gm/cm³. Find density at cross section 2.

• A. 16 gm/cm³
• B. 20 gm/cm³
• C. 24 gm/cm³
• D. 12 gm/cm³

Answer 1

Answer: (A)

16 gm/cm³

Answer 2

The relationship between stress ($\sigma$), density ($\rho$), acceleration ($a$), and distance ($x$) in a rod under acceleration is given by $\frac{d\sigma}{dx} = \rho(x) a$. This means the slope of the stress-distance graph is directly proportional to the density at that point, given constant acceleration.

The graph shows the angles of the tangent to the stress-distance curve. Assuming the angles $37^\circ$ and $53^\circ$ are measured with respect to the horizontal axis (as this leads to one of the options):

At cross-section 1, the slope $m_1$ is $\tan(37^\circ)$. $m_1 = \tan(37^\circ) \approx \frac{3}{4}$ So, $\rho_1 a = \frac{3}{4}$. Given $\rho_1 = 9 \, \text{gm/cm}^3$: $9 a = \frac{3}{4} \implies a = \frac{3}{36} = \frac{1}{12} \, \text{cm/s}^2$

At cross-section 2, the slope $m_2$ is $\tan(53^\circ)$. $m_2 = \tan(53^\circ) \approx \frac{4}{3}$ So, $\rho_2 a = \frac{4}{3}$. Substituting the value of $a$: $\rho_2 \left(\frac{1}{12}\right) = \frac{4}{3}$ $\rho_2 = \frac{4}{3} \times 12 = 16 \, \text{gm/cm}^3$

Alternatively, we can use the ratio of slopes: $\frac{m_2}{m_1} = \frac{\rho_2 a}{\rho_1 a} = \frac{\rho_2}{\rho_1}$ $\frac{\tan(53^\circ)}{\tan(37^\circ)} = \frac{4/3}{3/4} = \frac{16}{9}$ $\frac{\rho_2}{9 \, \text{gm/cm}^3} = \frac{16}{9}$ $\rho_2 = 16 \, \text{gm/cm}^3$