Question
Question: Figure shows graph of angle of deviation v/s angle of incidence for a light ray. Incident ray goes f...
Figure shows graph of angle of deviation v/s angle of incidence for a light ray. Incident ray goes from medium 1(μ1) to medium 2(μ2).
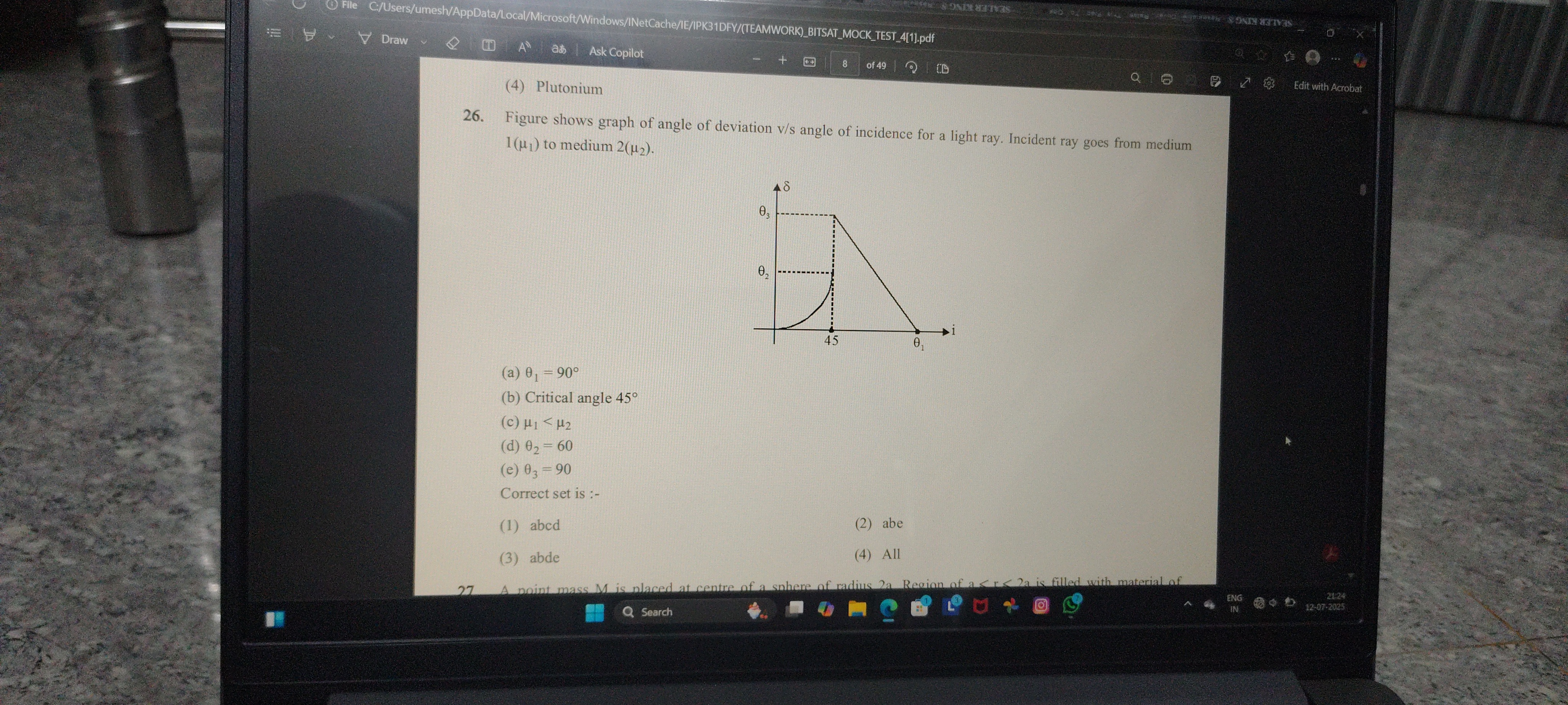
θ1 = 90°
Critical angle 45°
μ1<μ2
θ2 = 60
θ3 = 90
abe
Solution
The problem presents a graph of the angle of deviation (δ) versus the angle of incidence (i) for a light ray traveling from medium 1 (μ1) to medium 2 (μ2). We need to evaluate the correctness of five statements based on this graph.
Analysis of the graph:
- Region 1 (Refraction): The graph shows a curved path from i=0∘ to i=45∘. This corresponds to refraction. At i=0∘ (normal incidence), δ=0∘, which is expected.
- Region 2 (Total Internal Reflection - TIR): At i=45∘, the nature of the graph changes abruptly, and for i>45∘, it becomes a straight line with a negative slope. This change indicates that i=45∘ is the critical angle (ic), and for angles of incidence greater than ic, Total Internal Reflection (TIR) occurs. The straight line represents deviation during TIR.
(b) Critical angle 45°: As observed from the graph, the transition from refraction to TIR occurs at i=45∘. Therefore, the critical angle (ic) is 45∘. This statement is correct.
(c) μ1<μ2: For Total Internal Reflection (TIR) to occur, light must travel from a denser medium to a rarer medium. Since TIR is observed in the graph, it implies that medium 1 is denser than medium 2, i.e., μ1>μ2. From the critical angle, sinic=μ1μ2. sin45∘=21. So, μ1μ2=21, which means μ1=2μ2. This confirms μ1>μ2. This statement is incorrect.
(a) θ1=90∘: The graph for TIR extends up to θ1. The maximum possible angle of incidence is 90∘ (grazing incidence). At this angle, the ray is incident parallel to the interface. For TIR, this ray would also undergo reflection. Thus, θ1 represents the maximum possible angle of incidence, which is 90∘. This statement is correct.
(d) θ2=60: θ2 is the angle of deviation at the critical angle (ic=45∘). When light goes from a denser medium (μ1) to a rarer medium (μ2), it bends away from the normal, so the angle of refraction (r) is greater than the angle of incidence (i). The deviation is δ=r−i. At the critical angle, i=ic=45∘, and the angle of refraction r=90∘. Therefore, θ2=δ(ic)=r−ic=90∘−45∘=45∘. Since θ2=45∘, the statement θ2=60 is incorrect.
(e) θ3=90: θ3 is the angle of deviation when i=θ1=90∘.
Therefore, the correct set of statements is (a), (b), and (e).
