Question
Question: P is an orthogonal matrix of order 3 and $\alpha, \beta, \gamma$ are direction angles of a straight ...
P is an orthogonal matrix of order 3 and α,β,γ are direction angles of a straight line.
Let A=sin2αsinαsinβsinαsinγsinαsinβsin2βsinβsinγsinαsinγsinβsinγsin2γ and Q=PTAP. If PQ6PT=2kA, then k=
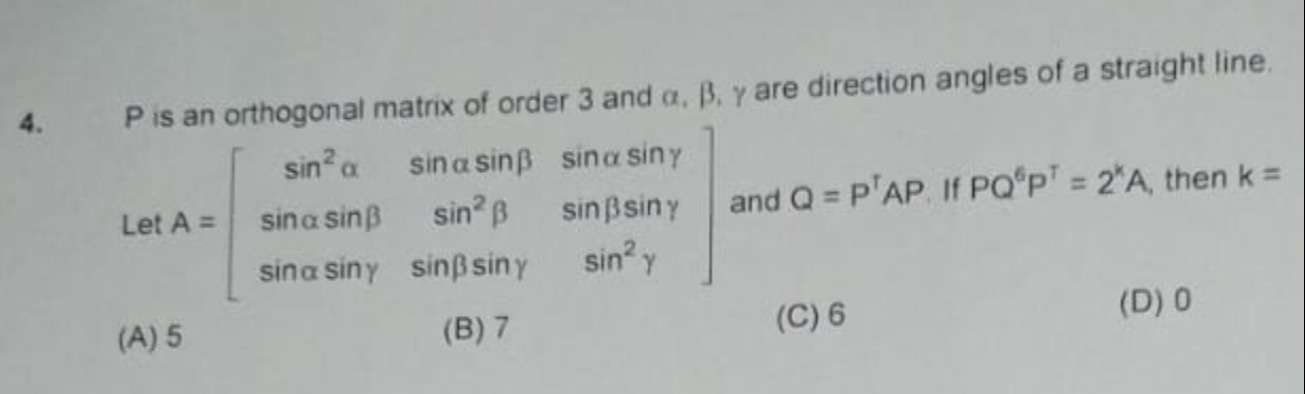
5
7
6
0
5
Solution
The problem asks us to find the value of k given an orthogonal matrix P, direction angles α,β,γ, and matrices A and Q. The relationship to be satisfied is PQ6PT=2kA.
1. Simplify PQ6PT using the properties of orthogonal matrices:
Given Q=PTAP. We need to calculate Qn. Let's find the first few powers of Q:
Q2=(PTAP)(PTAP)=PTA(PPT)AP. Since P is an orthogonal matrix, PPT=I (identity matrix). So, Q2=PTA(I)AP=PTA2P.
Similarly, Q3=Q⋅Q2=(PTAP)(PTA2P)=PTA(PPT)A2P=PTA(I)A2P=PTA3P.
By induction, we can generalize this to Qn=PTAnP. For n=6, we have Q6=PTA6P.
Now, substitute Q6 back into the expression PQ6PT:
PQ6PT=P(PTA6P)PT. Rearranging the terms: PQ6PT=(PPT)A6(PPT). Again, using PPT=I: PQ6PT=IA6I=A6.
So, the given equation simplifies to A6=2kA.
2. Analyze matrix A and calculate its powers:
The matrix A is given as: A=sin2αsinαsinβsinαsinγsinαsinβsin2βsinβsinγsinαsinγsinβsinγsin2γ
This matrix can be expressed as an outer product of a vector X with itself. Let X=sinαsinβsinγ. Then A=XXT.
XXT=sinαsinβsinγ[sinαsinβsinγ]=sin2αsinβsinαsinγsinαsinαsinβsin2βsinγsinβsinαsinγsinβsinγsin2γ, which matches A.
Now, let's calculate A2: A2=(XXT)(XXT)=X(XTX)XT. We need to calculate the scalar product XTX:
XTX=[sinαsinβsinγ]sinαsinβsinγ=sin2α+sin2β+sin2γ.
We are given that α,β,γ are direction angles of a straight line. This means their cosines are direction cosines, and they satisfy the relation: cos2α+cos2β+cos2γ=1.
Now, substitute sin2θ=1−cos2θ into the expression for XTX:
XTX=(1−cos2α)+(1−cos2β)+(1−cos2γ)
XTX=3−(cos2α+cos2β+cos2γ)
Using the direction angles property: XTX=3−1=2.
Now substitute this value back into the expression for A2: A2=X(2)XT=2(XXT)=2A.
3. Generalize An and find A6:
We found A2=2A. Let's find higher powers:
A3=A⋅A2=A⋅(2A)=2A2=2(2A)=22A.
A4=A⋅A3=A⋅(22A)=22A2=22(2A)=23A.
Following this pattern, we can see that An=2n−1A.
For n=6: A6=26−1A=25A.
4. Solve for k:
We have PQ6PT=A6 and A6=25A. The problem states PQ6PT=2kA. Therefore, 25A=2kA.
Since α,β,γ are direction angles, it's impossible for all sinα,sinβ,sinγ to be zero (as that would imply cos2α=1,cos2β=1,cos2γ=1, leading to 1+1+1=1, which is false). Thus, X is not a zero vector, and A is not a zero matrix.
Since A=0, we can compare the coefficients of A: 25=2k. This implies k=5.
