Question
Question: ${ }^{n}C_1 - (1+\frac{1}{2}){ }^{n}C_2 + (1+\frac{1}{2}+\frac{1}{3}){ }^{n}C_3 - (1+\frac{1}{2}+\fr...
nC1−(1+21)nC2+(1+21+31)nC3−(1+21+31+41)nC4+...+(−1)n−1(1+21+31+...+n1)nCn=
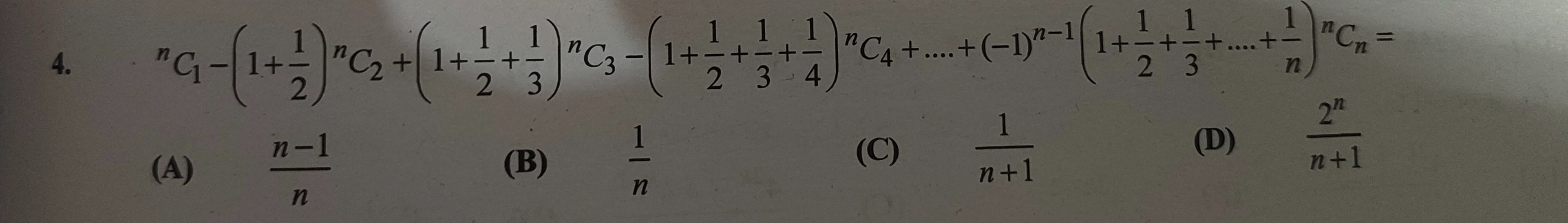
A
nn−1
B
n1
C
n+11
D
n+12n
Answer
n1
Explanation
Solution
We are given
S=k=1∑n(−1)k−1(1+21+31+⋯+k1)(kn).Notice that the harmonic number Hk=∑j=1kj1. Thus,
S=k=1∑n(−1)k−1Hk(kn)=k=1∑n(−1)k−1(kn)(j=1∑kj1).Interchange the order of summation:
S=j=1∑nj1k=j∑n(−1)k−1(kn).Using the known binomial identity
k=j∑n(−1)k−1(kn)=(−1)j−1(j−1n−1),we have
S=j=1∑nj(−1)j−1(j−1n−1).Let m=j−1 so that m=0 to n−1. Then,
S=m=0∑n−1m+1(−1)m(mn−1).It is known that
m=0∑Nm+1(−1)m(mN)=N+11,where here N=n−1. Therefore,
S=n1.