Question

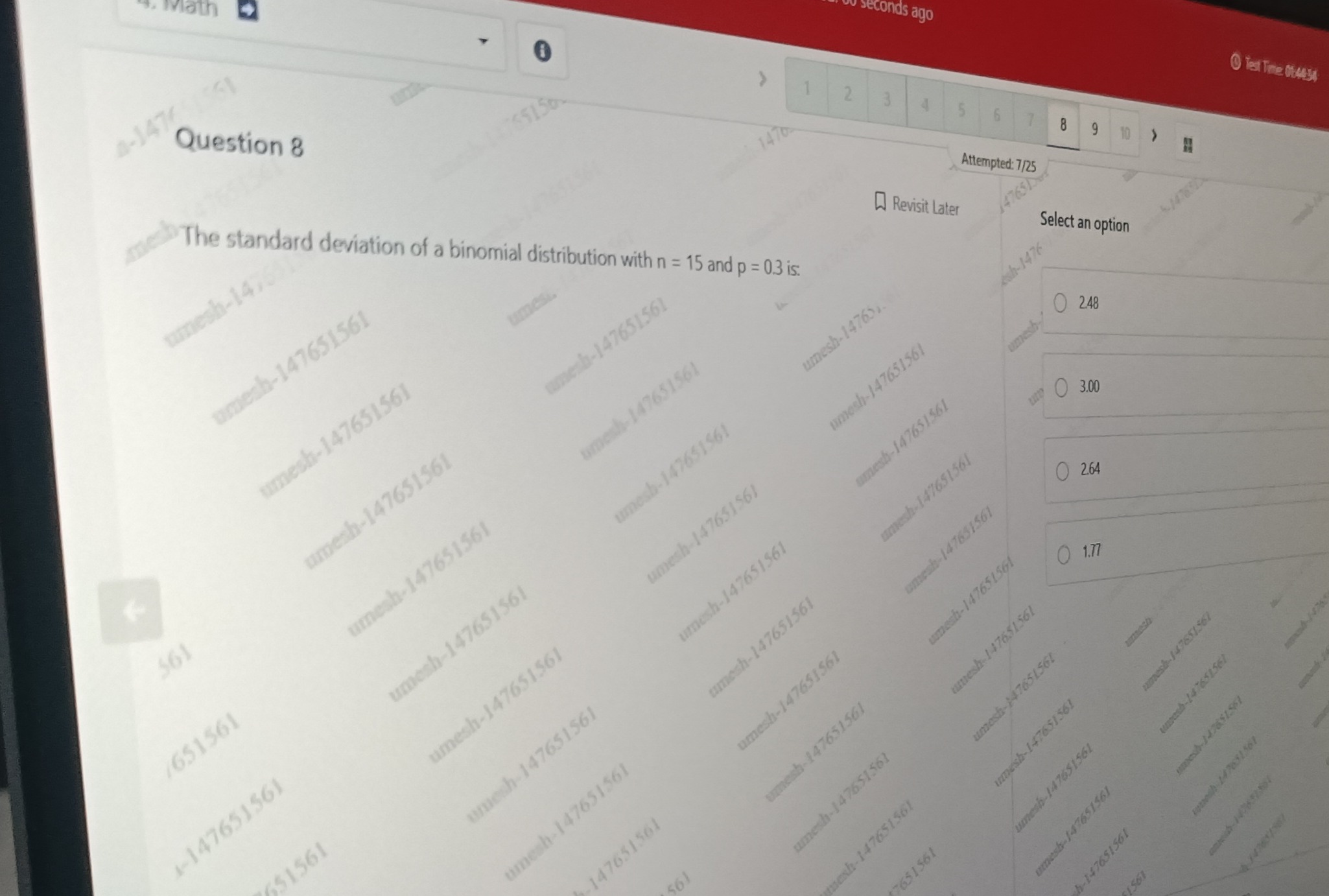
The standard deviation of a binomial distribution with n = 15 and p = 0.3 is:

• A. 2.48
• B. 3.00
• C. 2.64
• D. 1.77

Answer 1

Answer: (D)

1.77

Answer 2

For a binomial distribution, the number of trials is denoted by 'n', the probability of success in a single trial is 'p', and the probability of failure is 'q = 1 - p'.

The variance ($\sigma^2$) of a binomial distribution is given by the formula:

$\sigma^2 = npq$

The standard deviation ($\sigma$) is the square root of the variance:

$\sigma = \sqrt{npq}$

Given values:

n = 15 p = 0.3

Calculate q:

q = 1 - p = 1 - 0.3 = 0.7

Substitute the values into the standard deviation formula:

$\sigma = \sqrt{15 \times 0.3 \times 0.7}$ $\sigma = \sqrt{4.5 \times 0.7}$ $\sigma = \sqrt{3.15}$ $\sigma \approx 1.7748$

Rounding to two decimal places, the standard deviation is 1.77.