Question

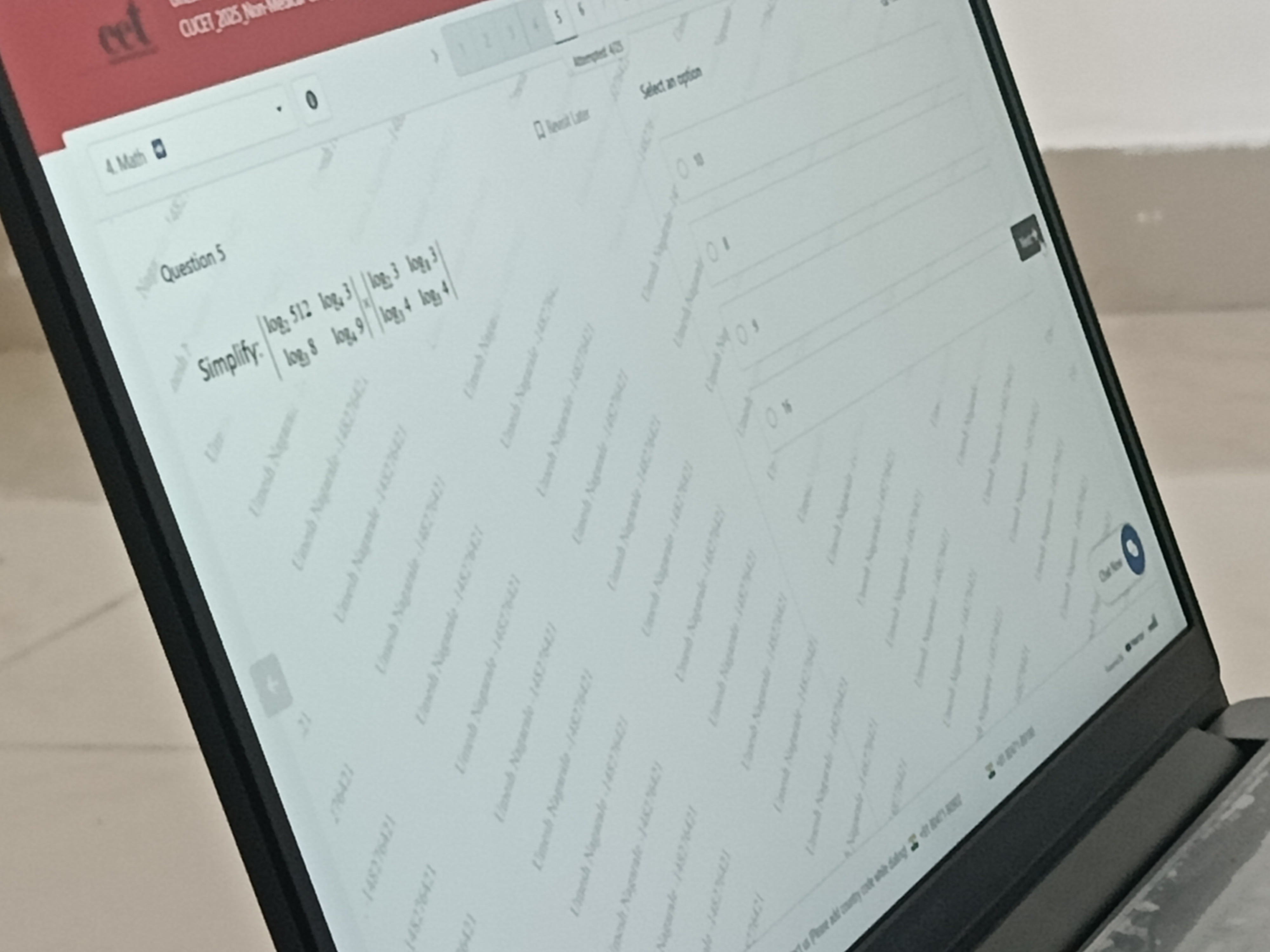
Simplify: $\frac{\log_2 512}{\log_3 8} \log_3 9 \frac{\log_3 3}{\log_3 4} \log_4 4$

• A. 10
• B. 1
• C. 9
• D. 16

Answer 1

None of the options provided are correct based on the exact expression.

Answer 2

To simplify the given expression, we evaluate each logarithmic term:

1. $\log_2 512 = 9$ since $512 = 2^9$.
2. $\log_3 8 = 3 \log_3 2$ since $8 = 2^3$.
3. $\log_3 9 = 2$ since $9 = 3^2$.
4. $\log_3 3 = 1$.
5. $\log_3 4 = 2 \log_3 2$ since $4 = 2^2$.
6. $\log_4 4 = 1$.

Substituting these values back into the original expression:

$$\frac{9}{3 \log_3 2} \times 2 \times \frac{1}{2 \log_3 2} \times 1 = \frac{18}{6 (\log_3 2)^2} = \frac{3}{(\log_3 2)^2}$$

Using the change of base rule $\log_b a = \frac{1}{\log_a b}$, we get:

$$\frac{3}{(\frac{1}{\log_2 3})^2} = 3 (\log_2 3)^2$$

Since $\log_2 3$ is an irrational number, $3 (\log_2 3)^2$ is also irrational. The options provided are integers, indicating an inconsistency between the question and the options. Therefore, none of the provided options are correct.