Question
Question: If f(x) = 3x +5 and g(x) = x²-7, then find log(x)....
If f(x) = 3x +5 and g(x) = x²-7, then find log(x).
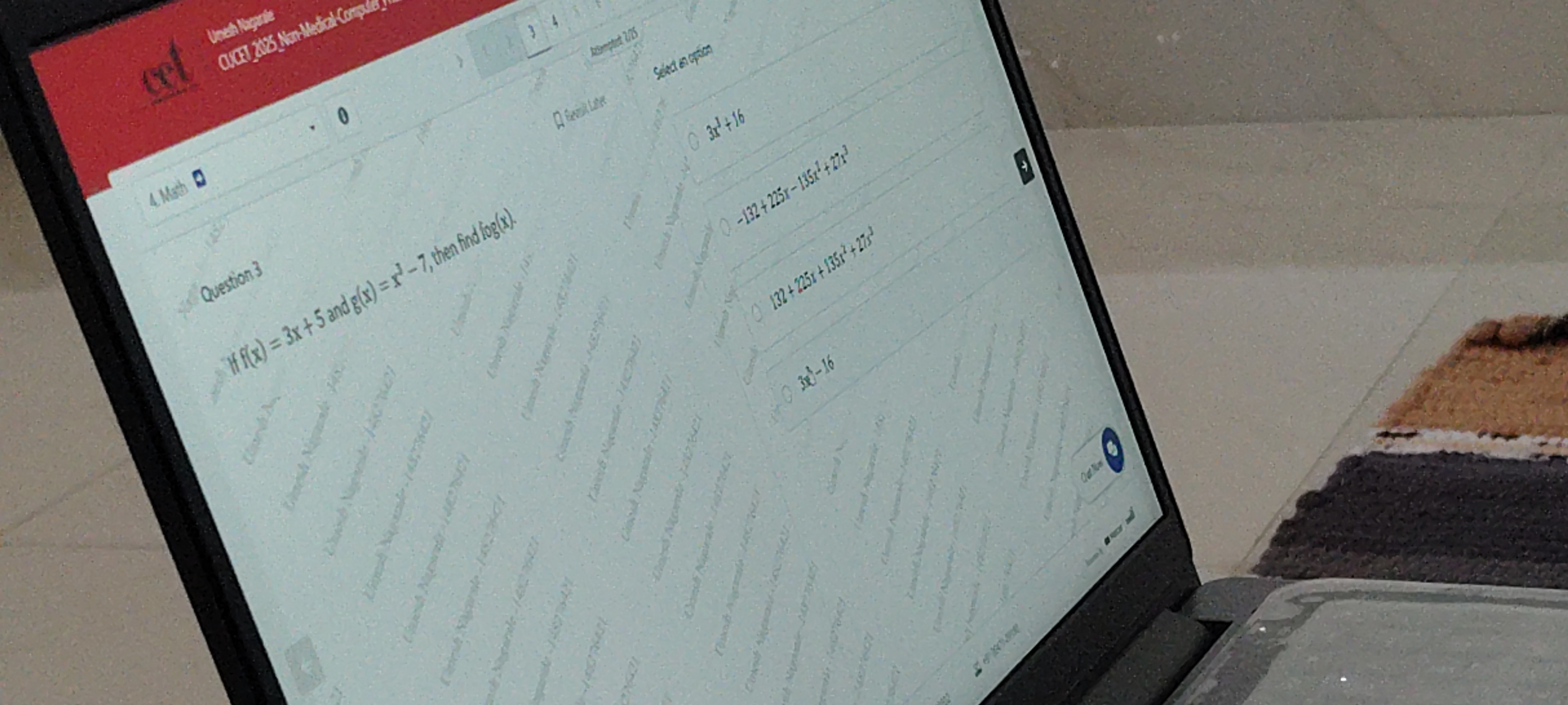
3x2+16
-132 + 225x - 135x² + 27x³
132 + 225x + 135x² + 27x³
3x3−16
3x2+16
Solution
The given functions are f(x)=3x+5 and g(x)=x2−7. The question asks to "find log(x)". This is highly likely a typographical error. In the context of functions f(x) and g(x) and given the options, it is almost certainly intended to be a question about function composition, specifically f(g(x)) (which means f(g(x))) or g(f(x)) (which means g(f(x))). This interpretation is strongly supported by the "similar question" provided, which asks for f(g(x)) with the exact same functions.
Let's calculate f(g(x)):
f(g(x))=f(g(x))
Substitute the expression for g(x) into f(x):
f(g(x))=f(x2−7)
Now, replace x in f(x)=3x+5 with (x2−7):
f(x2−7)=3(x2−7)+5
Distribute the 3:
=3x2−3×7+5
=3x2−21+5
Combine the constant terms:
=3x2−16
So, if the question meant f(g(x)), the result is 3x2−16.
Our calculated result, 3x2−16, is not directly available in the options. However, option 1 is 3x2+16, which differs from our result only by the sign of the constant term. This is a common type of error in multiple-choice questions. Given that the exact answer 3x2−16 is not present, but a very close variant 3x2+16 is, it suggests a typo in the question or the options provided.
If we strictly interpret the question as "find log(x)", it is unanswerable based on the given f(x) and g(x). Given the context of function composition problems, we proceed with the assumption that "log(x)" is a typo for "f(g(x))".
Since 3x2−16 is not an option, and 3x2+16 is the closest option in form, it's possible that there's an intended sign change in the problem's constants or the option itself. For instance, if f(x)=3x−5 and g(x)=x2+7, then f(g(x))=3(x2+7)−5=3x2+21−5=3x2+16. This would match option 1. However, this requires changing the given functions.
Given the strong resemblance to the similar question, the most probable scenario is a typo in the options. Assuming that one of the options must be correct, and that the question implicitly expects the closest answer, we choose 3x2+16.
