Question

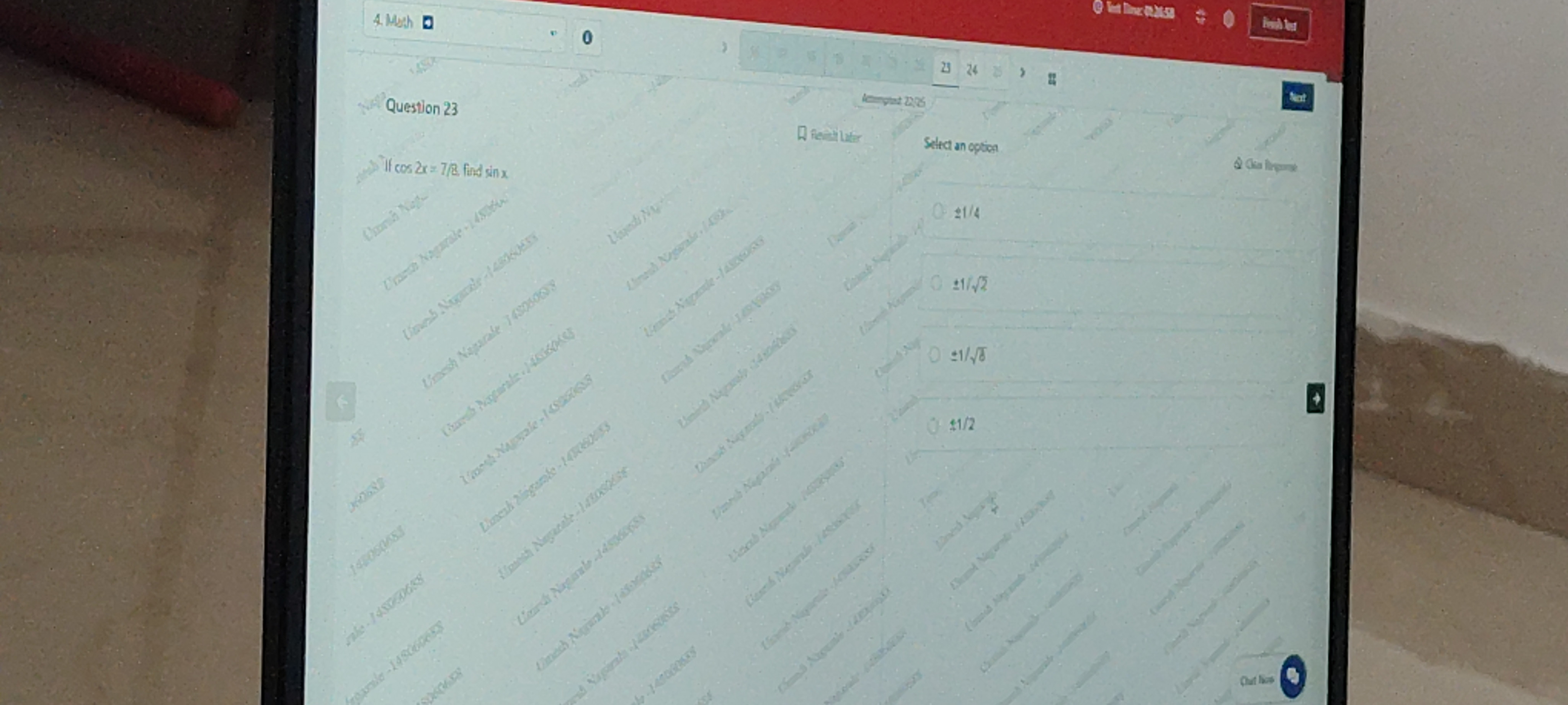
If cos 2x = 7/8 find sin x

• A. $\pm 1/4$
• B. $\pm 1/\sqrt{2}$
• C. $\pm 1/\sqrt{8}$
• D. $\pm 1/2$

Answer 1

Answer: (A)

$\pm 1/4$

Answer 2

The problem asks us to find the value of $\sin x$ given $\cos 2x = 7/8$.

We use the double angle identity for cosine, which relates $\cos 2x$ to $\sin x$: $\cos 2x = 1 - 2\sin^2 x$

Substitute the given value of $\cos 2x$ into the identity: $\frac{7}{8} = 1 - 2\sin^2 x$

Now, we need to solve for $\sin x$. First, rearrange the equation to isolate $2\sin^2 x$: $2\sin^2 x = 1 - \frac{7}{8}$

To subtract the fractions on the right side, find a common denominator: $2\sin^2 x = \frac{8}{8} - \frac{7}{8}$ $2\sin^2 x = \frac{1}{8}$

Next, divide both sides by 2 to find $\sin^2 x$: $\sin^2 x = \frac{1}{8 \times 2}$ $\sin^2 x = \frac{1}{16}$

Finally, take the square root of both sides to find $\sin x$: $\sin x = \pm \sqrt{\frac{1}{16}}$ $\sin x = \pm \frac{1}{4}$

The value of $\sin x$ is $\pm 1/4$.