Question

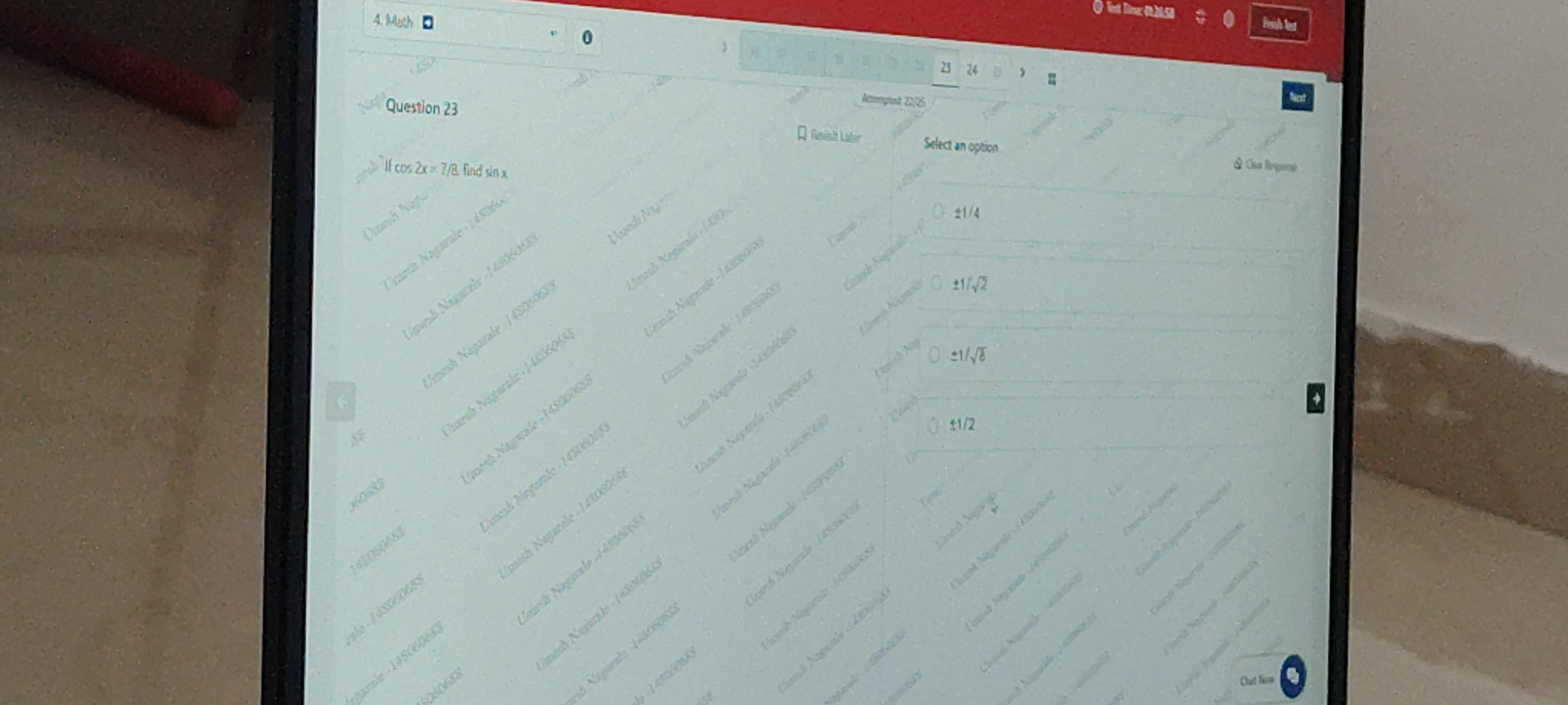
If cos 2x = 7/8 find sin x

• A. $\pm 1/4$
• B. $\pm 1/\sqrt{2}$
• C. $\pm 1/\sqrt{8}$
• D. $\pm 1/2$

Answer 1

Answer: (A)

$\pm 1/4$

Answer 2

We use the double angle identity for cosine that relates $\cos 2x$ to $\sin x$:

$\cos 2x = 1 - 2\sin^2 x$

Substitute the given value of $\cos 2x = 7/8$ into the identity:

$7/8 = 1 - 2\sin^2 x$

Now, we need to solve this equation for $\sin x$. Rearrange the equation to isolate $2\sin^2 x$:

$2\sin^2 x = 1 - 7/8$ $2\sin^2 x = (8 - 7)/8$ $2\sin^2 x = 1/8$

Divide both sides by 2:

$\sin^2 x = \frac{1/8}{2}$ $\sin^2 x = 1/16$

Take the square root of both sides to find $\sin x$:

$\sin x = \pm \sqrt{1/16}$ $\sin x = \pm 1/4$