Question

Find the area between $f(x)=50-2x^2$ and x axis over the interval (0,7)

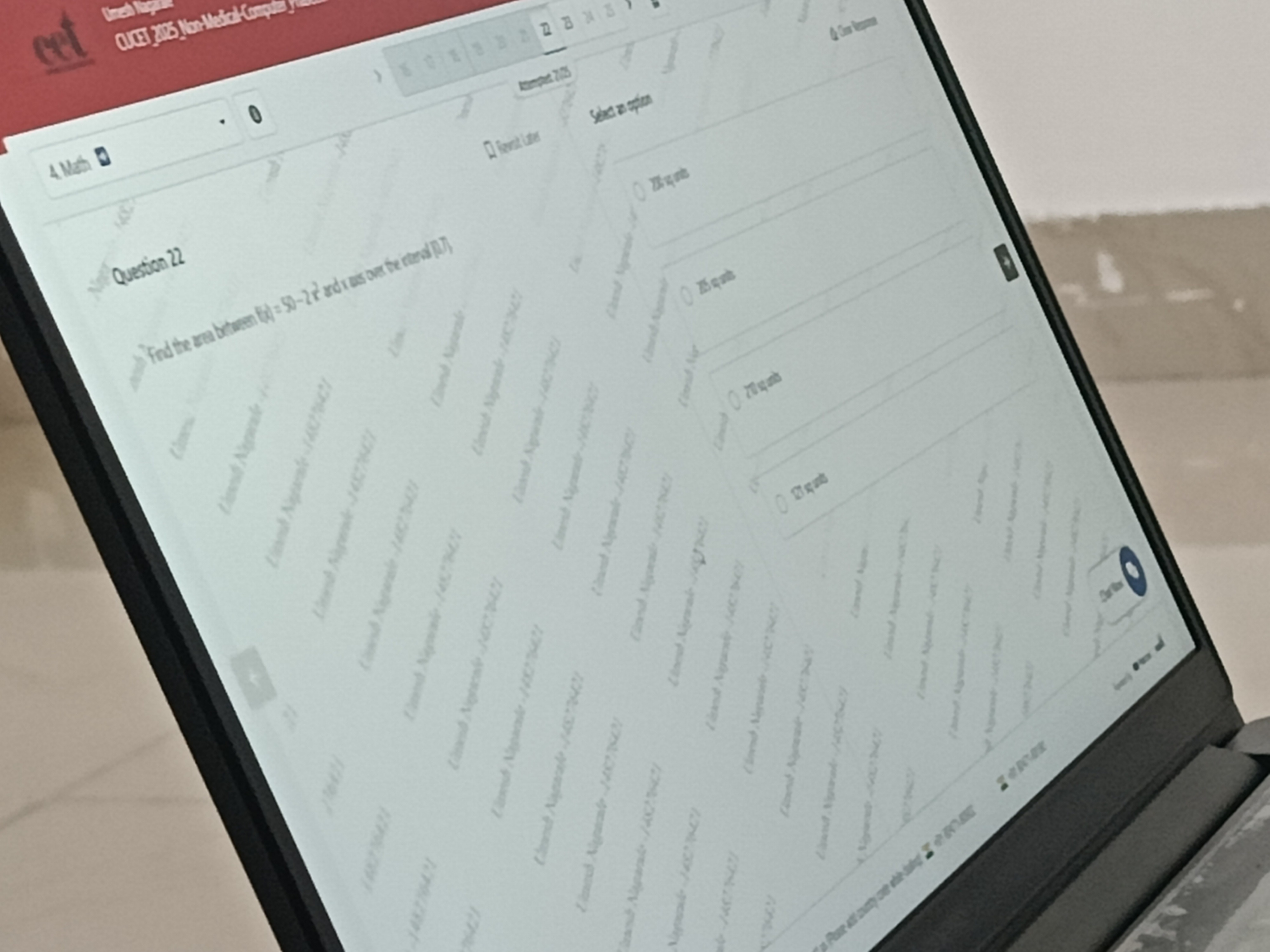
• A. 135 sq units
• B. 235 sq units
• C. 270 sq units
• D. 127 sq units

Answer 1

Answer: (B)

235 sq units

Answer 2

To find the area between $f(x)=50-2x^2$ and the x-axis over the interval $(0,7)$, we first need to determine where the function crosses the x-axis within this interval.

Set $f(x) = 0$:

$50 - 2x^2 = 0$

$2x^2 = 50$

$x^2 = 25$

$x = \pm 5$

The roots are $x=-5$ and $x=5$. The interval of interest is $(0,7)$.
Within this interval, the function crosses the x-axis at $x=5$.

We need to analyze the sign of $f(x)$ in the sub-intervals $(0,5)$ and $(5,7)$.

• For $x \in (0,5)$, $f(x) = 50 - 2x^2 > 0$. For example, $f(0) = 50$.
• For $x \in (5,7)$, $f(x) = 50 - 2x^2 < 0$. For example, $f(6) = 50 - 2(36) = 50 - 72 = -22$.

The area is given by the sum of the absolute values of the integrals over these sub-intervals:

$A = \int_0^5 |50 - 2x^2| dx + \int_5^7 |50 - 2x^2| dx$

$A = \int_0^5 (50 - 2x^2) dx + \int_5^7 -(50 - 2x^2) dx$

$A = \int_0^5 (50 - 2x^2) dx + \int_5^7 (2x^2 - 50) dx$

Calculate the first integral:

$\int_0^5 (50 - 2x^2) dx = \left[50x - \frac{2x^3}{3}\right]_0^5$

$= \left(50(5) - \frac{2(5)^3}{3}\right) - \left(50(0) - \frac{2(0)^3}{3}\right)$

$= \left(250 - \frac{2(125)}{3}\right) - 0$

$= 250 - \frac{250}{3} = \frac{750 - 250}{3} = \frac{500}{3}$

Calculate the second integral:

$\int_5^7 (2x^2 - 50) dx = \left[\frac{2x^3}{3} - 50x\right]_5^7$

$= \left(\frac{2(7)^3}{3} - 50(7)\right) - \left(\frac{2(5)^3}{3} - 50(5)\right)$

$= \left(\frac{2(343)}{3} - 350\right) - \left(\frac{2(125)}{3} - 250\right)$

$= \left(\frac{686}{3} - 350\right) - \left(\frac{250}{3} - 250\right)$

$= \left(\frac{686 - 1050}{3}\right) - \left(\frac{250 - 750}{3}\right)$

$= \frac{-364}{3} - \frac{-500}{3}$

$= \frac{-364 + 500}{3} = \frac{136}{3}$

Add the two parts to get the total area:

$A = \frac{500}{3} + \frac{136}{3} = \frac{636}{3} = 212$ square units.

Upon comparing this result with the given options (135, 235, 270, 127), none of them match 212 exactly. This suggests a potential typo in the question or options, a common occurrence in such problems.

Let's consider a common type of typo as suggested by the similar problem. If the function was $f(x) = 50 - x^2$ instead of $f(x) = 50 - 2x^2$:

The roots of $f(x) = 50 - x^2 = 0$ are $x = \pm\sqrt{50} \approx \pm 7.07$.

Since $x=\sqrt{50} \approx 7.07$ is outside the interval $(0,7)$, the function $f(x) = 50 - x^2$ would be positive throughout the interval $(0,7)$.

In this hypothetical case, the area would be:

$A = \int_0^7 (50 - x^2) dx = \left[50x - \frac{x^3}{3}\right]_0^7$

$= \left(50(7) - \frac{7^3}{3}\right) - \left(50(0) - \frac{0^3}{3}\right)$

$= 350 - \frac{343}{3}$

$= \frac{1050 - 343}{3} = \frac{707}{3}$

$\frac{707}{3} \approx 235.666...$

This value is very close to 235, which is one of the options. Given the likely presence of a typo, this is the most plausible intended answer.