Question

If P(A∪B) = 0.8, P(A) = 0.5, and P(B) = 0.6, what is P(A∩B)?

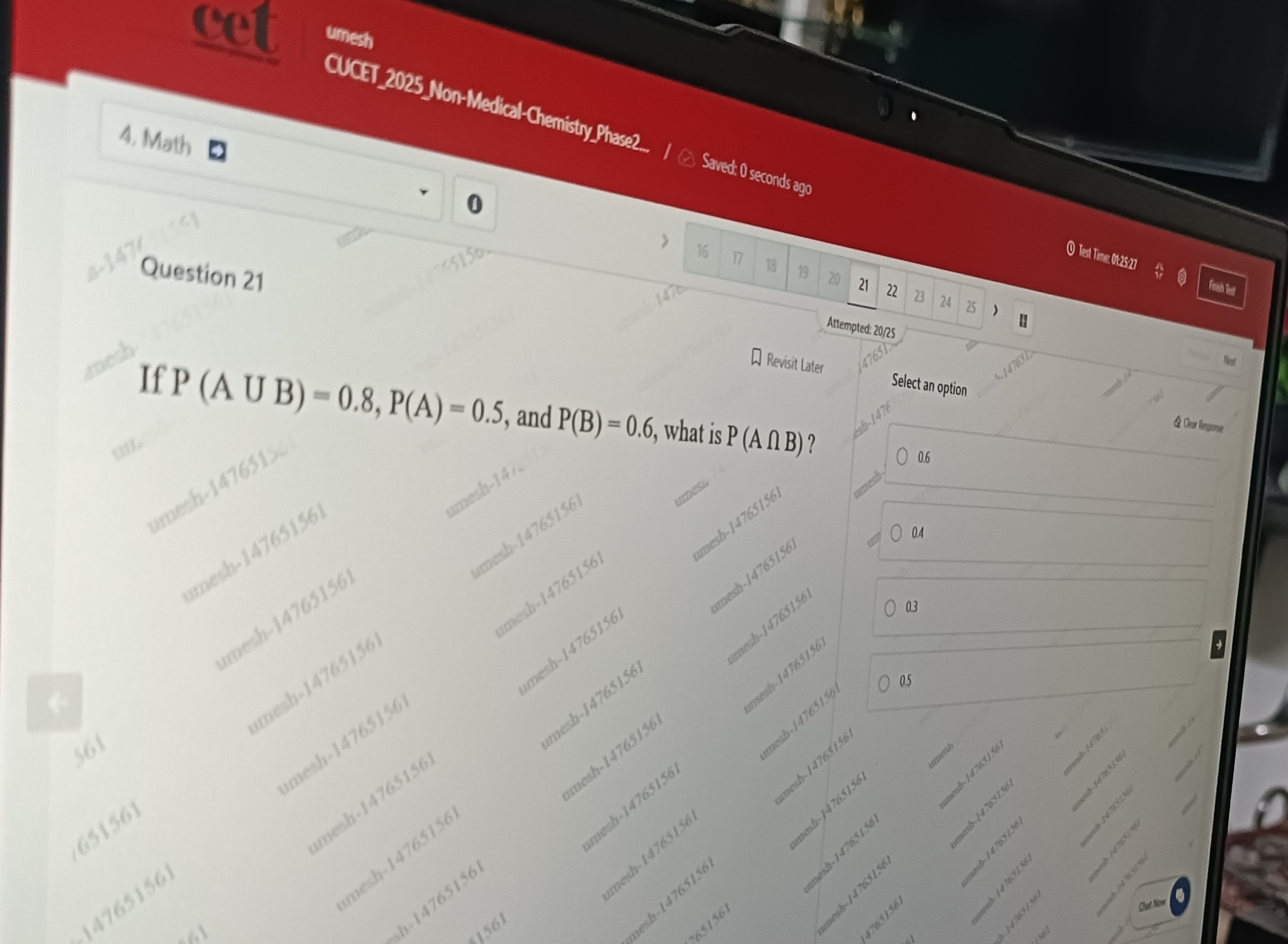
• A. 0.6
• B. 0.4
• C. 0.3
• D. 0.5

Answer 1

Answer: (C)

0.3

Answer 2

We are given the probabilities of the union of two events, P(A∪B), and the individual probabilities of the events, P(A) and P(B). We need to find the probability of the intersection of two events, P(A∩B).

We use the formula:

$P(A \cup B) = P(A) + P(B) - P(A \cap B)$

We are given:

• $P(A \cup B) = 0.8$
• $P(A) = 0.5$
• $P(B) = 0.6$

We can rearrange the formula to solve for $P(A \cap B)$:

$P(A \cap B) = P(A) + P(B) - P(A \cup B)$

Substitute the given values:

$P(A \cap B) = 0.5 + 0.6 - 0.8$ $P(A \cap B) = 1.1 - 0.8$ $P(A \cap B) = 0.3$

Thus, the probability of the intersection of events A and B is 0.3.