Question

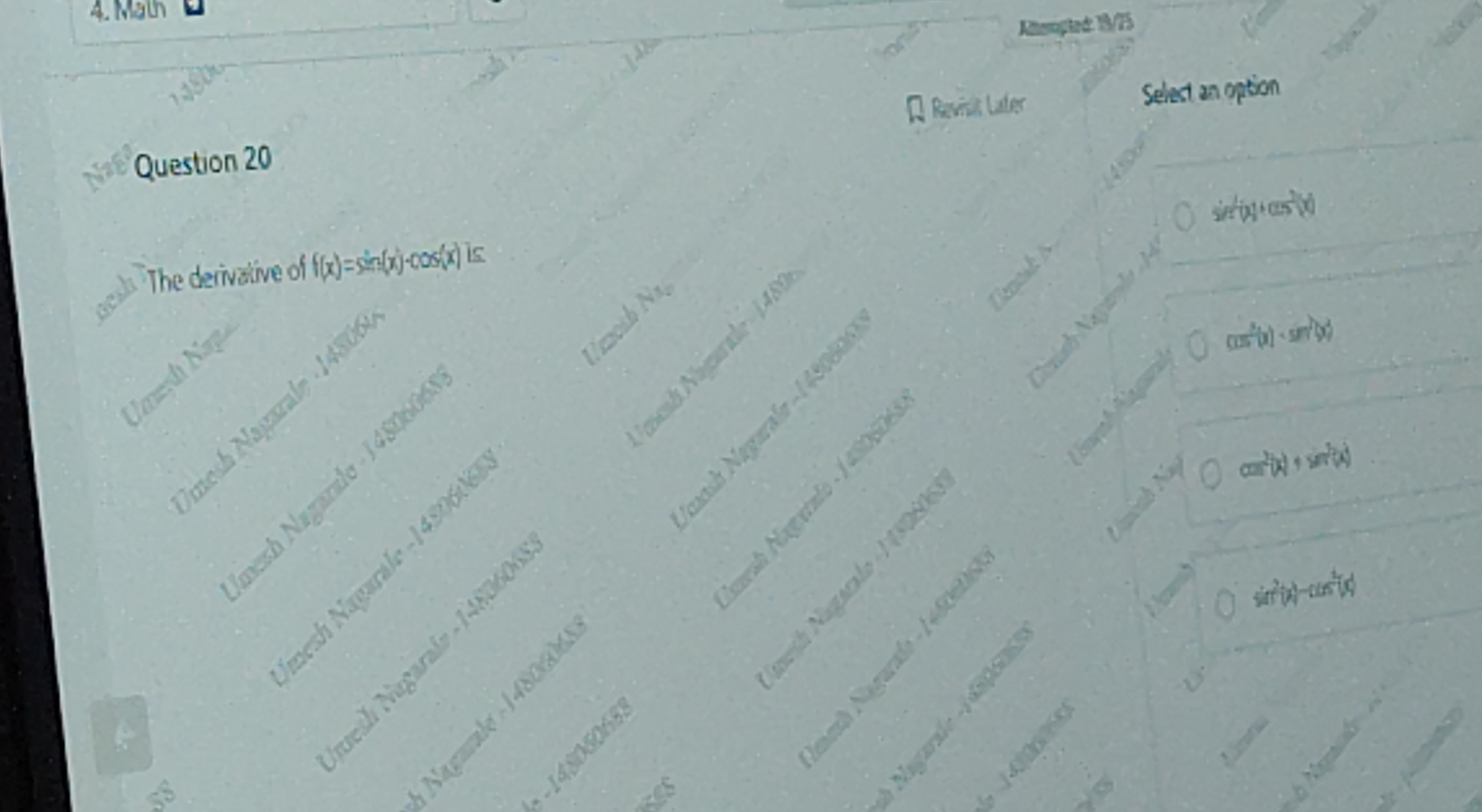
The derivative of f(x)=sin(x)-cos(x) is

• A. $\sin^2(x)+\cos^2(x)$
• B. $\cos^2(x)-\sin^2(x)$
• C. $\cos^2(x)+\sin^2(x)$
• D. $\sin^2(x)-\cos^2(x)$

Answer 1

Answer: (D)

$\sin^2(x)-\cos^2(x)$

Answer 2

To find the derivative of the function $f(x) = \sin(x) - \cos(x)$, we apply the rules of differentiation:

• The derivative of $\sin(x)$ is $\cos(x)$.
• The derivative of $\cos(x)$ is $-\sin(x)$.

Using the linearity property of derivatives, which states that $\frac{d}{dx}(u(x) - v(x)) = \frac{d}{dx}(u(x)) - \frac{d}{dx}(v(x))$:

$f'(x) = \frac{d}{dx}(\sin(x) - \cos(x))$ $f'(x) = \frac{d}{dx}(\sin(x)) - \frac{d}{dx}(\cos(x))$ $f'(x) = \cos(x) - (-\sin(x))$ $f'(x) = \cos(x) + \sin(x)$

The calculated derivative, $\cos(x) + \sin(x)$, does not match any of the provided options.

However, considering a potential misphrasing in the question, if it intended to ask for $f(x) \cdot f'(x)$, then:

$f(x) \cdot f'(x) = (\sin(x) - \cos(x))(\sin(x) + \cos(x)) = \sin^2(x) - \cos^2(x)$.

This matches option 4.