Question

If the third term of a G.P. is 4 then the product of its first 5 terms is

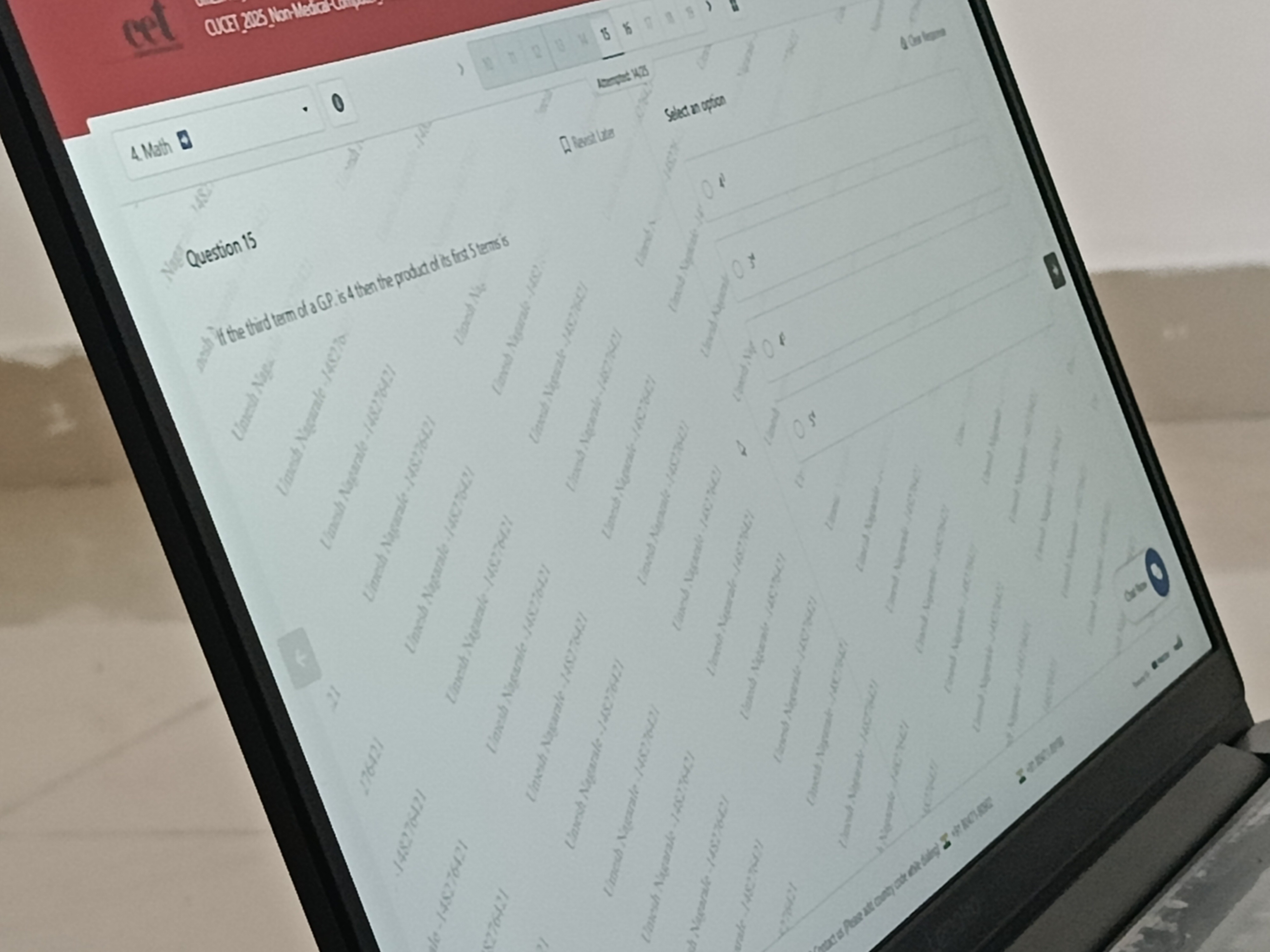
• A. 4
• B. 32
• C. 4^5
• D. 16

Answer 1

Answer: (C)

4^5

Answer 2

Let the first term of the G.P. be 'a' and the common ratio be 'r'.
The terms of the G.P. are:

1. First term ($a_1$): $a$
2. Second term ($a_2$): $ar$
3. Third term ($a_3$): $ar^2$
4. Fourth term ($a_4$): $ar^3$
5. Fifth term ($a_5$): $ar^4$

We are given that the third term of the G.P. is 4. So, $a_3 = ar^2 = 4$.

We need to find the product of its first 5 terms, let's call it P.
$P = a_1 \times a_2 \times a_3 \times a_4 \times a_5$
Substitute the expressions for each term:
$P = a \times (ar) \times (ar^2) \times (ar^3) \times (ar^4)$

Now, group the 'a' terms and the 'r' terms:
$P = (a \times a \times a \times a \times a) \times (r \times r^2 \times r^3 \times r^4)$
$P = a^5 \times r^{(1+2+3+4)}$
$P = a^5 \times r^{10}$

We can rewrite $a^5 r^{10}$ as $(ar^2)^5$.
We know from the given information that $ar^2 = 4$.
Substitute this value into the product expression:
$P = (4)^5$

Thus, the product of the first 5 terms is $4^5$.