Question
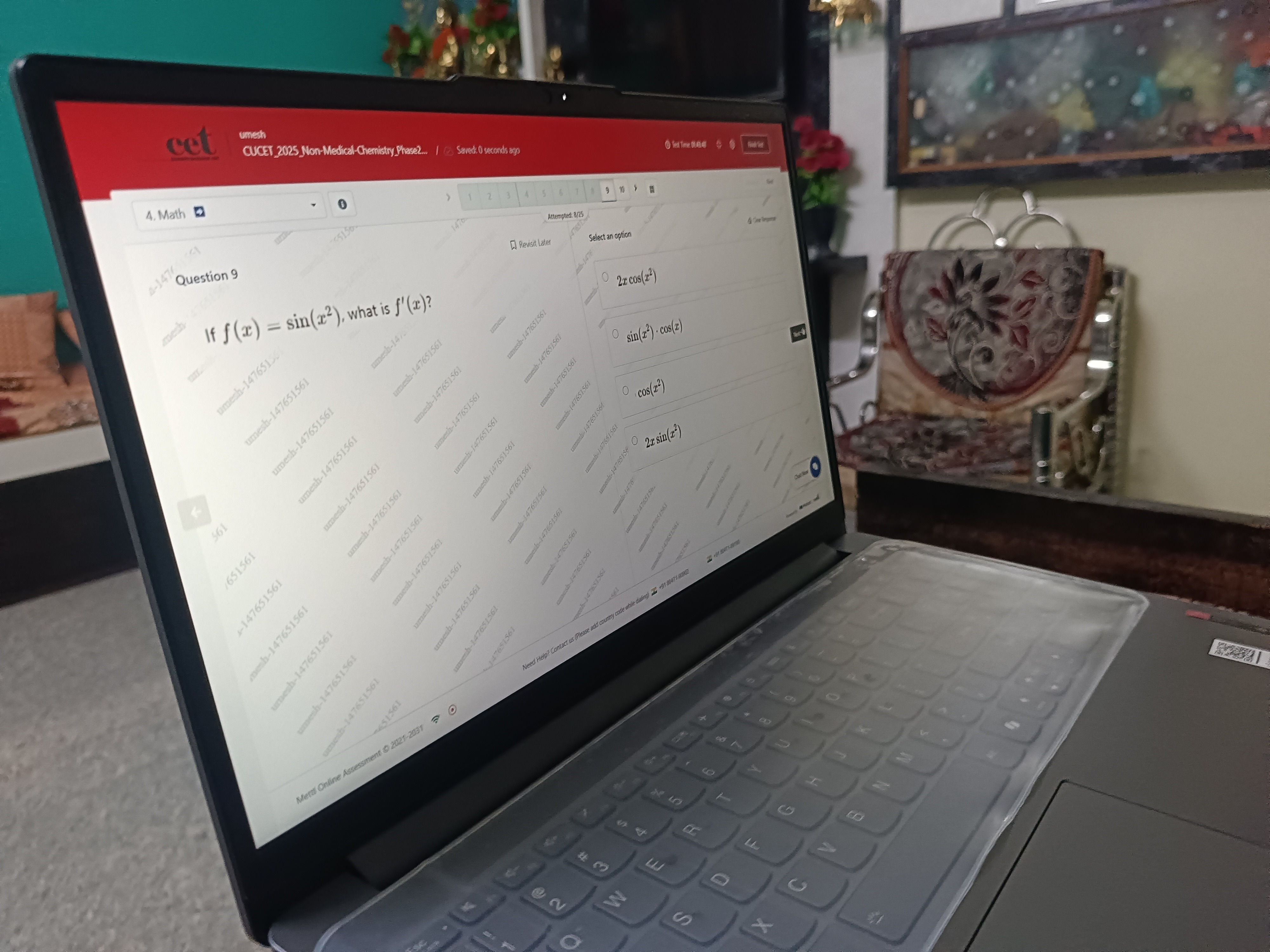
Question: If $f(x) = sin(x^2)$, what is $f'(x)$?...
If f(x)=sin(x2), what is f′(x)?
A
2xcos(x2)
B
sin(x2)⋅cos(x)
C
cos(x2)
D
2xsin(x2)
Answer
2xcos(x2)
Explanation
Solution
To find the derivative of f(x)=sin(x2), we use the chain rule.
Let y=f(x)=sin(x2). We can consider this as a composite function where y=sin(u) and u=x2.
According to the chain rule, dxdy=dudy⋅dxdu.
First, find the derivative of y with respect to u: dudy=dud(sin(u))=cos(u)
Next, find the derivative of u with respect to x: dxdu=dxd(x2)=2x
Now, substitute u=x2 back into cos(u) and multiply the two derivatives: f′(x)=cos(x2)⋅(2x) f′(x)=2xcos(x2)
