Question
Question: Let $\vec{a} = \hat{i}-\hat{j}, \vec{b} = \hat{j}-\hat{k}, \vec{c} = \hat{k}-\hat{i}$. If $\hat{d}$ ...
Let a=i^−j^,b=j^−k^,c=k^−i^. If d^ is a unit vector such that a⋅d^=0=[bcd^], then d^ equals :
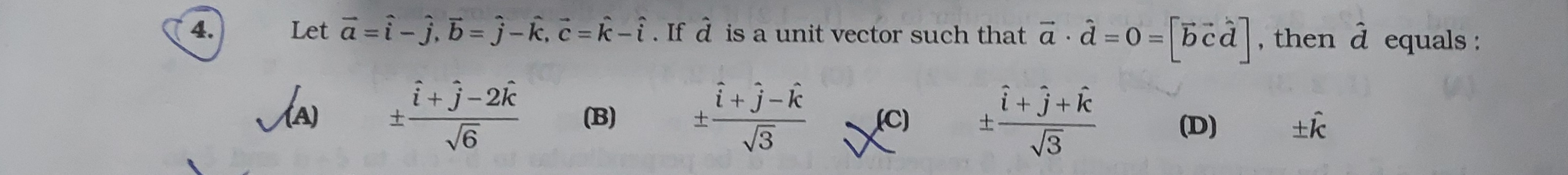
6i^+j^−2k^
3i^+j^−k^
3i^+j^+k^
k^
±6i^+j^−2k^
Solution
The given conditions are:
- a⋅d^=0: This implies that the unit vector d^ is orthogonal to the vector a.
- [bcd^]=0: This is the scalar triple product of b, c, and d^. A zero scalar triple product means the three vectors are coplanar. This implies that d^ is orthogonal to the vector formed by the cross product of b and c, i.e., d^⊥(b×c).
Given vectors: a=i^−j^ b=j^−k^ c=k^−i^
First, calculate the cross product b×c: b×c=(j^−k^)×(k^−i^) b×c=i^0−1j^10k^−11=i^(1−0)−j^(0−1)+k^(0−(−1))=i^+j^+k^ Let v=b×c=i^+j^+k^.
Now, d^ must be orthogonal to both a and v. Therefore, d^ must be parallel to the cross product of a and v. Calculate a×v: a×v=(i^−j^)×(i^+j^+k^) a×v=i^11j^−11k^01=i^(−1−0)−j^(1−0)+k^(1−(−1))=−i^−j^+2k^
Since d^ is a unit vector, it must be in the direction of a×v or its opposite direction, with a magnitude of 1. d^=±∣−i^−j^+2k^∣−i^−j^+2k^ The magnitude is: ∣−i^−j^+2k^∣=(−1)2+(−1)2+(2)2=1+1+4=6 So, d^=±6−i^−j^+2k^=±6i^+j^−2k^ This matches option (A).
