Question

Let PG is the normal at point P to a parabola cuts its axis in G and is produced to Q so that GQ = 1/2PG. The other normals which pass through Q intersect at an angle of $\pi/k$, then k= tangents to the parabola $y^2 = 4ax$ which with the

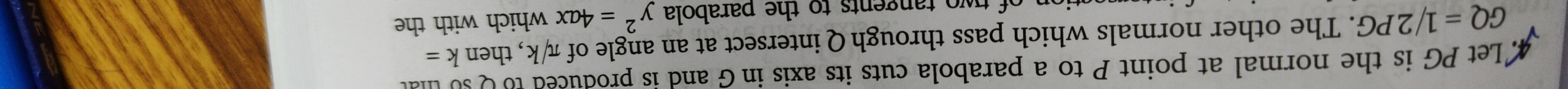
• A. 2
• B. 3
• C. 4
• D. 1

Answer 1

Answer: (A)

2

Answer 2

The normal at $P(at^2, 2at)$ to the parabola $y^2 = 4ax$ is given by $y - 2at = -t(x - at^2)$, which simplifies to $y = -tx + at^3 + 2at$. This normal intersects the axis of the parabola ($y=0$) at point $G$. Setting $y=0$, we get $0 = -tx_G + at^3 + 2at$, so $x_G = at^2 + 2a$. Thus, $G = (at^2 + 2a, 0)$.

The point $Q$ is obtained by producing $PG$ such that $GQ = \frac{1}{2}PG$. This means $Q$ lies on the line $PG$ and $G$ is between $P$ and $Q$. The coordinates of $Q$ can be found using the section formula or vector addition. If $\vec{P}$ and $\vec{G}$ are the position vectors of $P$ and $G$, then $\vec{Q} = \vec{G} + \frac{1}{2}(\vec{G} - \vec{P}) = \frac{3}{2}\vec{G} - \frac{1}{2}\vec{P}$. $x_Q = \frac{3}{2}(at^2 + 2a) - \frac{1}{2}(at^2) = \frac{3}{2}at^2 + 3a - \frac{1}{2}at^2 = at^2 + 3a$. $y_Q = \frac{3}{2}(0) - \frac{1}{2}(2at) = -at$. So, $Q = (at^2 + 3a, -at)$.

Now, let $t_1$ be the parameter of another normal passing through $Q$. The equation of this normal is $y = -t_1 x + at_1^3 + 2at_1$. Substituting the coordinates of $Q$: $-at = -t_1(at^2 + 3a) + at_1^3 + 2at_1$ $-at = -at_1 t^2 - 3at_1 + at_1^3 + 2at_1$ $-at = -at_1 t^2 - at_1 + at_1^3$ Dividing by $a$ (assuming $a \neq 0$): $-t = -t_1 t^2 - t_1 + t_1^3$ $t_1^3 - t^2 t_1 - t_1 + t = 0$ $t_1^3 - (t^2+1)t_1 + t = 0$.

We know that $t_1 = t$ is one root since the normal at $P$ passes through $Q$. Factoring out $(t_1 - t)$: $(t_1 - t)(t_1^2 + tt_1 - 1) = 0$. The other normals passing through $Q$ have parameters $t_2$ and $t_3$, which are the roots of the quadratic equation $t_1^2 + tt_1 - 1 = 0$. The slopes of these two normals are $m_2 = -t_2$ and $m_3 = -t_3$. The product of these slopes is $m_2 m_3 = (-t_2)(-t_3) = t_2 t_3$. From the quadratic equation $t_1^2 + tt_1 - 1 = 0$, the product of the roots $t_2 t_3 = \frac{-1}{1} = -1$. Since the product of the slopes of the two other normals is $-1$, these normals are perpendicular to each other. The angle between them is $\frac{\pi}{2}$. The problem states that this angle is $\frac{\pi}{k}$. Therefore, $\frac{\pi}{2} = \frac{\pi}{k}$, which implies $k=2$.