Question
Question: Let $P_n(x)$ be a function satisfying $\sum_{n=0}^{\infty} h^nP_n(x) = (1-2hx+h^2)^{-1/2}, |x| \leq ...
Let Pn(x) be a function satisfying ∑n=0∞hnPn(x)=(1−2hx+h2)−1/2,∣x∣≤1,∣h∣<1/3. Then the unit digit of, P3(10), is
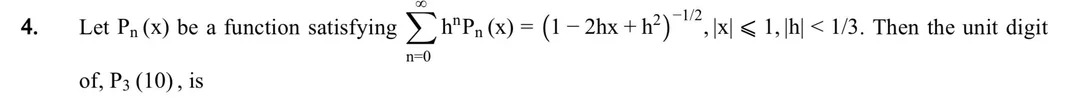
5
Solution
The given generating function is: ∑n=0∞hnPn(x)=(1−2hx+h2)−1/2 This is the generating function for Legendre polynomials, Pn(x). We need to find the unit digit of P3(10).
We can find P3(x) by expanding the given generating function using the binomial theorem. Recall the binomial expansion: (1−u)−1/2=1+21u+21232!1u2+2123253!1u3+… (1−u)−1/2=1+21u+83u2+165u3+… Let u=2hx−h2. Substitute this into the expansion: (1−2hx+h2)−1/2=1+21(2hx−h2)+83(2hx−h2)2+165(2hx−h2)3+… We are looking for P3(x), which is the coefficient of h3. Let's expand the terms and collect the coefficients of h3:
-
From the first term: 1 (coefficient of h0)
-
From the second term: 21(2hx−h2)=hx−21h2. No h3 term here.
-
From the third term: 83(2hx−h2)2 83(2hx−h2)2=83((2hx)2−2(2hx)(h2)+(h2)2) =83(4h2x2−4h3x+h4) The term with h3 is 83(−4h3x)=−23h3x. So, the coefficient of h3 from this term is −23x.
-
From the fourth term: 165(2hx−h2)3 165(2hx−h2)3=165((2hx)3−3(2hx)2(h2)+3(2hx)(h2)2−(h2)3) We only need the term with h3. This comes from the first part of the expansion (2hx)3: 165(2hx)3=165(8h3x3)=25h3x3 So, the coefficient of h3 from this term is 25x3. Higher terms in the expansion like h4,h5,h6 will not contribute to P3(x).
Combining the coefficients of h3 from all terms, we get P3(x): P3(x)=25x3−23x P3(x)=21(5x3−3x)
Now, we need to find P3(10): P3(10)=21(5(10)3−3(10)) P3(10)=21(5(1000)−30) P3(10)=21(5000−30) P3(10)=21(4970) P3(10)=2485 The unit digit of P3(10) is 5.
