Question

Let $\hat{a}+2\hat{b}+\hat{c}=\hat{a}\times\hat{c}$ then $|\hat{a}\times\hat{b}+\hat{b}\times\hat{c}+\hat{a}+\hat{b}+\hat{c}|$ is equal to

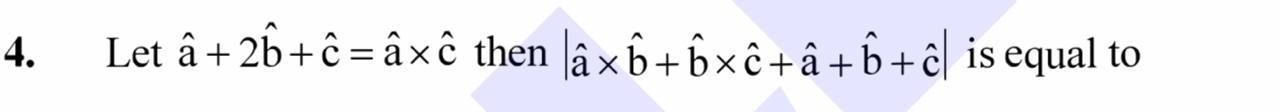
Answer 1

1

Answer 2

1. Dot product of given equation with $\hat{a}$ and $\hat{c}$ gives two equations.

2. Squaring the given equation yields an equation in $\hat{a}\cdot\hat{c}$ (B) leading to $B=1$.

3. Then, $2A+1=-1$ gives $A=-1$ (and similarly $C=-1$).

4. Since $B=1$, $\hat{a}$ and $\hat{c}$ are parallel; thus, $\hat{c} = \hat{a}$ and $\hat{b} = -\hat{a}$.

5. Substituting in the target expression gives $\hat{a}$ with magnitude 1.