Question

Let $f(x) = \frac{1}{x+1}$ and $f(g(x)) = \frac{x-1}{x}$ then the value of $\int_{2}^{1} g(f(x))\,dx$ is equal to

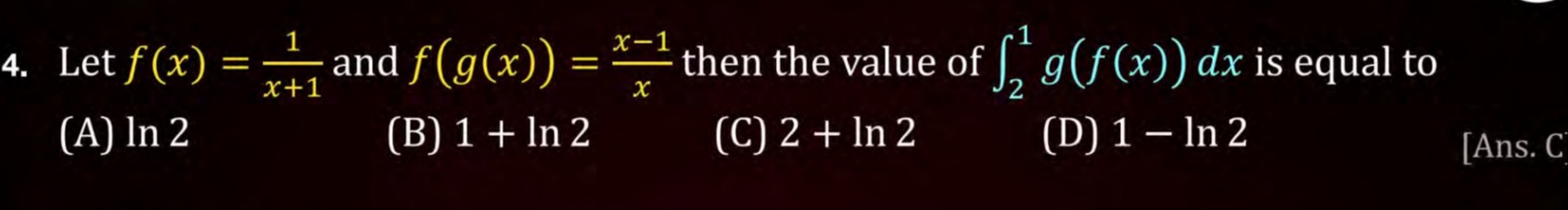
• A. ln 2
• B. 1 + ln 2
• C. 2 + ln 2
• D. 1 − ln 2

Answer 1

Answer: (B)

1 + ln 2

Answer 2

First, find $g(x)$. We are given $f(x) = \frac{1}{x+1}$ and $f(g(x)) = \frac{x-1}{x}$. Since $f(g(x)) = \frac{1}{g(x)+1}$, we have $\frac{1}{g(x)+1} = \frac{x-1}{x}$. This implies $g(x)+1 = \frac{x}{x-1}$, so $g(x) = \frac{x}{x-1} - 1 = \frac{x-(x-1)}{x-1} = \frac{1}{x-1}$.

Next, find $g(f(x))$. Substitute $f(x) = \frac{1}{x+1}$ into $g(x) = \frac{1}{x-1}$: $g(f(x)) = g\left(\frac{1}{x+1}\right) = \frac{1}{\frac{1}{x+1} - 1} = \frac{1}{\frac{1 - (x+1)}{x+1}} = \frac{x+1}{1 - x - 1} = \frac{x+1}{-x} = -1 - \frac{1}{x}$.

Now, evaluate the integral $\int_{2}^{1} g(f(x))\,dx$: $\int_{2}^{1} \left(-1 - \frac{1}{x}\right)\,dx$. Using the property $\int_{a}^{b} h(x)\,dx = -\int_{b}^{a} h(x)\,dx$: $\int_{2}^{1} \left(-1 - \frac{1}{x}\right)\,dx = -\int_{1}^{2} \left(-1 - \frac{1}{x}\right)\,dx = \int_{1}^{2} \left(1 + \frac{1}{x}\right)\,dx$.

The antiderivative of $1 + \frac{1}{x}$ is $x + \ln|x|$. Evaluate the definite integral: $\left[x + \ln|x|\right]_{1}^{2} = (2 + \ln|2|) - (1 + \ln|1|) = (2 + \ln 2) - (1 + 0) = 1 + \ln 2$.