Question

Let $f(n) = \sum_{k=0}^{n} \binom{n}{k} \cos\bigl(\tfrac{2k\pi}{n}\bigr)$ and $g(n) = \sum_{k=0}^{n-1} \binom{n-1}{k} \cos\bigl(\tfrac{2k\pi}{n}\bigr)$, then

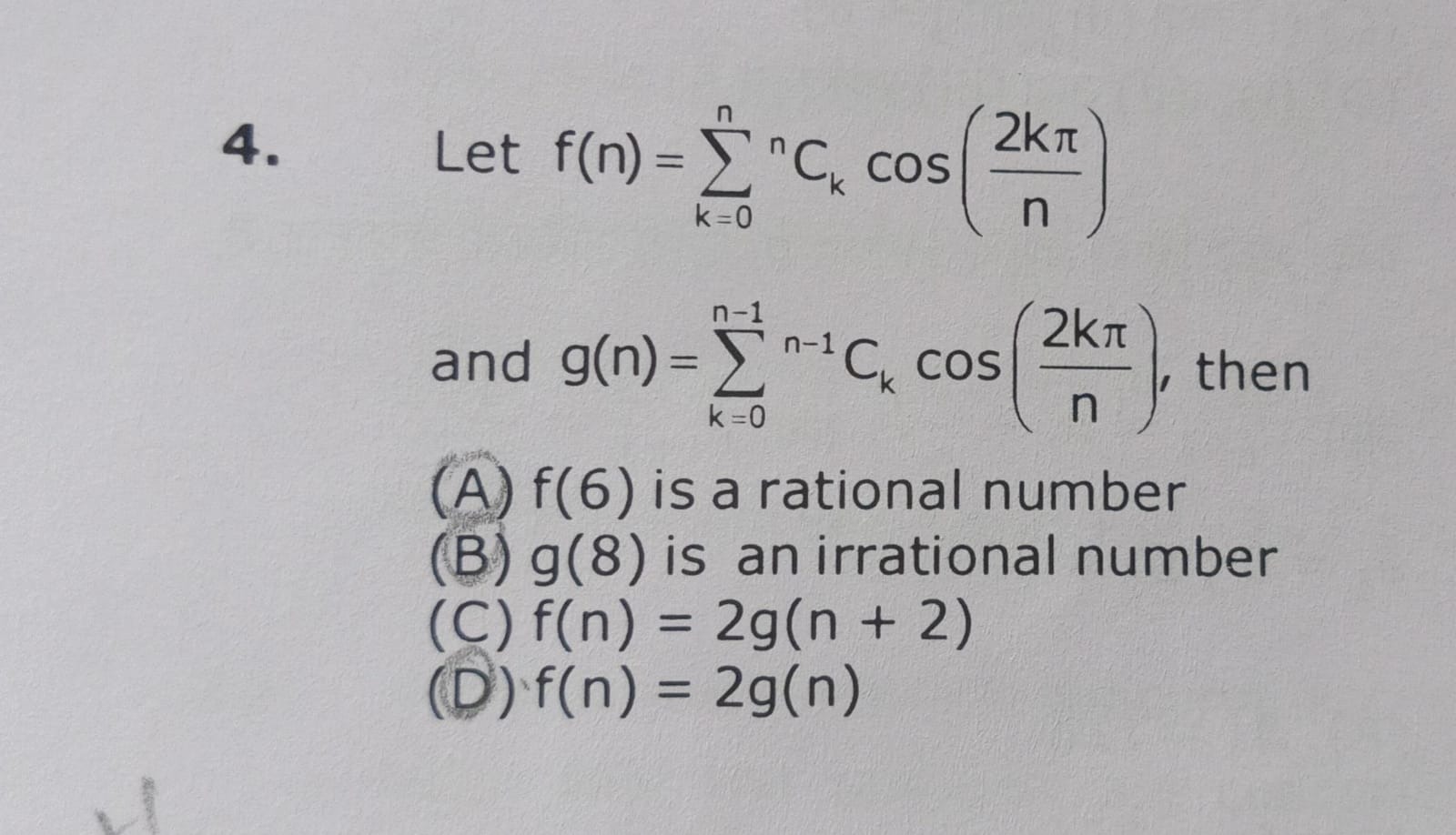
• A. f(6) is a rational number
• B. g(8) is an irrational number
• C. f(n) = 2g(n + 2)
• D. f(n) = 2g(n)

Answer 1

Answer: (A), (B), (D)

A, B, D

Answer 2

1. Expressing sums via complex expansion
Use the identity

$$(1 + e^{i\theta})^n = \sum_{k=0}^n \binom{n}{k} e^{ik\theta} = 2^n \cos^n\!\tfrac{\theta}{2}\;e^{i\,n\theta/2}.$$

Taking real parts with $\theta = \tfrac{2\pi}{n}$ gives

$$f(n) = \Re\bigl[(1+e^{i2\pi/n})^n\bigr] = \Re\!\bigl[2^n \cos^n(\tfrac{\pi}{n}) e^{i\pi}\bigr] = -2^n \cos^n\!\bigl(\tfrac{\pi}{n}\bigr).$$

2. Verifying option (A)

$$f(6) = -2^6 \cos^6\!\tfrac{\pi}{6} = -64\bigl(\tfrac{\sqrt3}{2}\bigr)^6 = -64\cdot\tfrac{27}{64} = -27,$$

which is rational. ✓

3. Expressing $g(n)$
Similarly,

$$g(n) = \Re\bigl[(1+e^{i2\pi/n})^{\,n-1}\bigr] =2^{\,n-1}\cos^{\,n-1}\!\bigl(\tfrac{\pi}{n}\bigr)\cos\!\bigl(\tfrac{(n-1)\pi}{n}\bigr).$$

Noting $\cos\bigl(\tfrac{(n-1)\pi}{n}\bigr)=-\cos(\tfrac{\pi}{n})$,

$$g(n)=-2^{\,n-1}\cos^n\!\bigl(\tfrac{\pi}{n}\bigr).$$

4. Verifying option (B)
For $n=8$,

$$g(8)=-2^7\cos^8\!\bigl(\tfrac\pi8\bigr) =-128\Bigl(\tfrac{\sqrt{2+\sqrt2}}{2}\Bigr)^8,$$

which is irrational. ✓

5. Relation between $f(n)$ and $g(n)$

$$2\,g(n)=2\bigl[-2^{n-1}\cos^n\!\tfrac{\pi}{n}\bigr] =-2^n\cos^n\!\tfrac{\pi}{n} =f(n).$$

So $f(n)=2g(n)$. Option (D) ✓, while (C) fails in general.