Question

In the given figure river water is flowing at 4 m/s. A boat is steered at angle $127^\circ$ from the direction of flow of river. Width of river is 1560 m, and velocity of boat in still water is 5 m/s. Find drift of boat in river (in km).

Answer 1

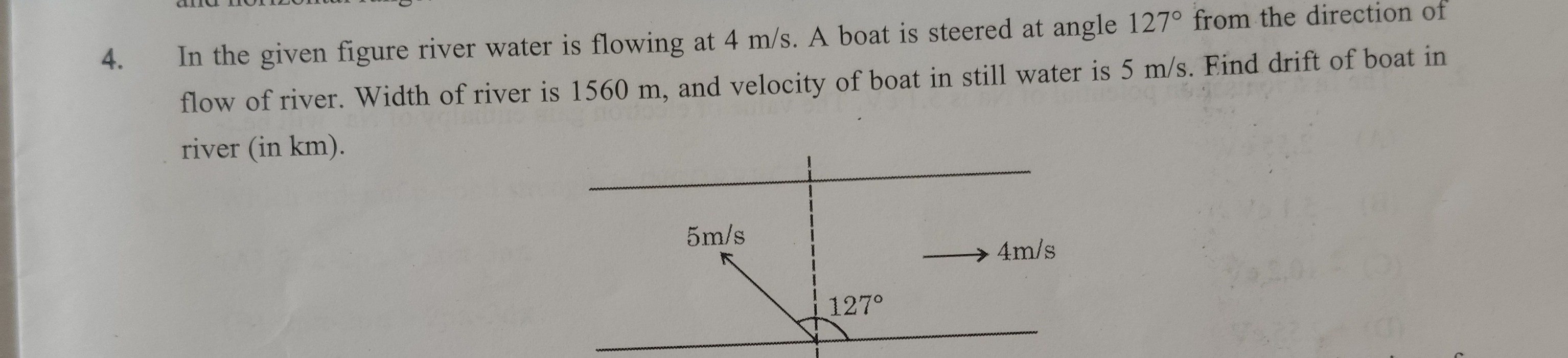
0.39

Answer 2

Let the river flow in the positive x-direction. The velocity of the river is $\vec{v}_r = 4 \hat{i}$ m/s.
The velocity of the boat in still water (velocity of boat relative to water) is $\vec{v}_{b/w}$. Its magnitude is $v_b = 5$ m/s. The angle of $\vec{v}_{b/w}$ with the direction of river flow (positive x-axis) is $127^\circ$.
The components of $\vec{v}_{b/w}$ are:
$v_{b/w, x} = v_b \cos(127^\circ) = 5 \cos(127^\circ)$
$v_{b/w, y} = v_b \sin(127^\circ) = 5 \sin(127^\circ)$

We use the trigonometric identities $\cos(180^\circ - \theta) = -\cos(\theta)$ and $\sin(180^\circ - \theta) = \sin(\theta)$.
$\cos(127^\circ) = \cos(180^\circ - 53^\circ) = -\cos(53^\circ)$
$\sin(127^\circ) = \sin(180^\circ - 53^\circ) = \sin(53^\circ)$

Using the approximate values for $\sin(53^\circ) \approx 4/5 = 0.8$ and $\cos(53^\circ) \approx 3/5 = 0.6$:
$v_{b/w, x} = 5 \times (-0.6) = -3$ m/s.
$v_{b/w, y} = 5 \times 0.8 = 4$ m/s.

The velocity of the boat relative to the ground is $\vec{v}_b = \vec{v}_{b/w} + \vec{v}_r$.
$\vec{v}_b = (-3 \hat{i} + 4 \hat{j}) + 4 \hat{i} = (4-3)\hat{i} + 4\hat{j} = 1 \hat{i} + 4 \hat{j}$ m/s.

The velocity component perpendicular to the banks (in the y-direction) is $v_{b,y} = 4$ m/s.
The width of the river is $w = 1560$ m.
The time taken to cross the river is $t = \frac{\text{width}}{v_{b,y}} = \frac{1560 \text{ m}}{4 \text{ m/s}} = 390$ seconds.

The velocity component parallel to the banks (in the x-direction) is $v_{b,x} = 1$ m/s.
The drift of the boat is the displacement in the x-direction during the time $t$.
Drift ($d$) = $v_{b,x} \times t = 1 \text{ m/s} \times 390 \text{ s} = 390$ meters.

The question asks for the drift in kilometers.
$d = 390 \text{ m} = \frac{390}{1000} \text{ km} = 0.390$ km.

The final answer is $0.39$.