Question
Question: The displacement vs time of a particle executing SHM is shown in figure. The initial phase $\phi$ is...
The displacement vs time of a particle executing SHM is shown in figure. The initial phase ϕ is
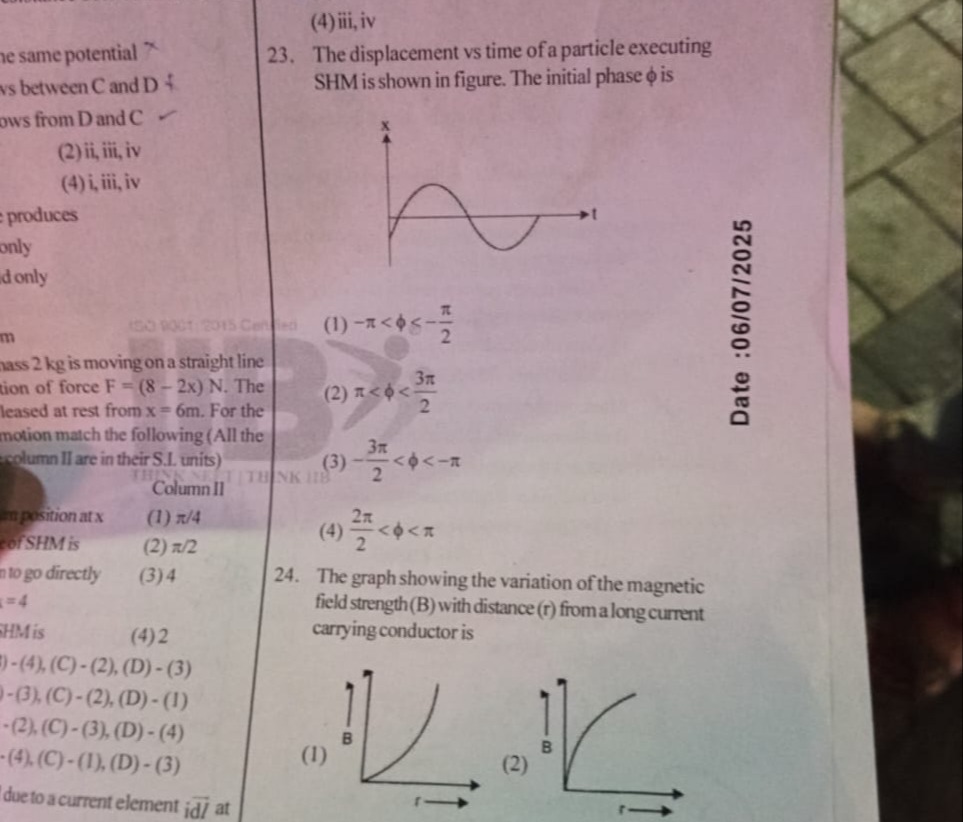
−π<ϕ<−2π
π<ϕ<23π
−23π<ϕ<−π
22π<ϕ<π
π<ϕ<23π
Solution
The general equation for the displacement of a particle executing SHM can be written as:
x(t)=Acos(ωt+ϕ)
From the given graph:
-
At t=0, the displacement x(0) is negative. Substituting t=0 into the equation: x(0)=Acos(ϕ) Since x(0)<0 and amplitude A>0, we must have cos(ϕ)<0. This implies that the initial phase ϕ must lie in the second or third quadrant (i.e., 2π<ϕ<23π).
-
At t=0, the slope of the x vs t graph is positive, which means the initial velocity v(0) is positive. The velocity v(t) is given by the derivative of x(t) with respect to t: v(t)=dtdx=−Aωsin(ωt+ϕ) Substituting t=0: v(0)=−Aωsin(ϕ) Since v(0)>0 and Aω>0, we must have −sin(ϕ)>0, which means sin(ϕ)<0. This implies that the initial phase ϕ must lie in the third or fourth quadrant (i.e., π<ϕ<2π or −π<ϕ<0).
Combining both conditions:
- cos(ϕ)<0 (Q2 or Q3)
- sin(ϕ)<0 (Q3 or Q4)
For both conditions to be satisfied simultaneously, the initial phase ϕ must be in the third quadrant. Therefore, the range for ϕ is π<ϕ<23π.
