Solveeit Logo
Login

Question

Question: If $|z_1|=1, |z_2|=2, |z_3|=3 \text{ and } |9z_1z_2+4z_1z_3+z_2z_3|=36$, then $|z_1+z_2+z_3|$ is equ...

If ∣z1∣=1,∣z2∣=2,∣z3∣=3 and ∣9z1z2+4z1z3+z2z3∣=36|z_1|=1, |z_2|=2, |z_3|=3 \text{ and } |9z_1z_2+4z_1z_3+z_2z_3|=36, then ∣z1+z2+z3∣|z_1+z_2+z_3| is equal to

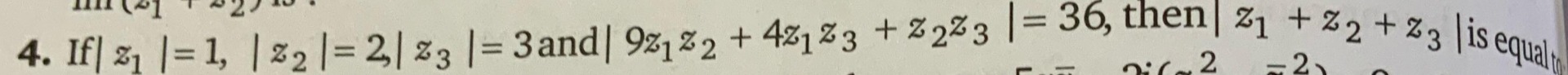
A

Z2

B

26~2

C
D

6

Answer

6 (Option d)

Explanation

Solution

Explanation:
Given

∣9z1z2+4z1z3+z2z3∣=36,|9z_1z_2+4z_1z_3+z_2z_3| = 36,

note that 9=∣z3∣29=|z_3|^2, 4=∣z2∣24=|z_2|^2, and 1=∣z1∣21=|z_1|^2. Rewriting the expression, we have

9z1z2+4z1z3+z2z3=z1z2z3(z1‾+z2‾+z3‾).9z_1z_2+4z_1z_3+z_2z_3 = z_1z_2z_3\left(\overline{z_1}+\overline{z_2}+\overline{z_3}\right).

Taking moduli gives

∣z1z2z3∣⋅∣z1‾+z2‾+z3‾∣=∣z1∣∣z2∣∣z3∣⋅∣z1+z2+z3∣=6∣z1+z2+z3∣.|z_1z_2z_3|\cdot|\overline{z_1}+\overline{z_2}+\overline{z_3}| = |z_1||z_2||z_3|\cdot|z_1+z_2+z_3| = 6|z_1+z_2+z_3|.

Since ∣z1∣=1|z_1|=1, ∣z2∣=2|z_2|=2, and ∣z3∣=3|z_3|=3 we have

6∣z1+z2+z3∣=36⇒∣z1+z2+z3∣=366=6.6|z_1+z_2+z_3| = 36 \quad\Rightarrow\quad |z_1+z_2+z_3| = \frac{36}{6} = 6.