Question
Question: If xf(x) = 3(f(x))² + 2, then $\int \frac{2x^2 - 12xf(x)+f(x)}{(6f(x)-x)(x^2-f(x))^2} dx$ equals to...
If xf(x) = 3(f(x))² + 2, then ∫(6f(x)−x)(x2−f(x))22x2−12xf(x)+f(x)dx equals to
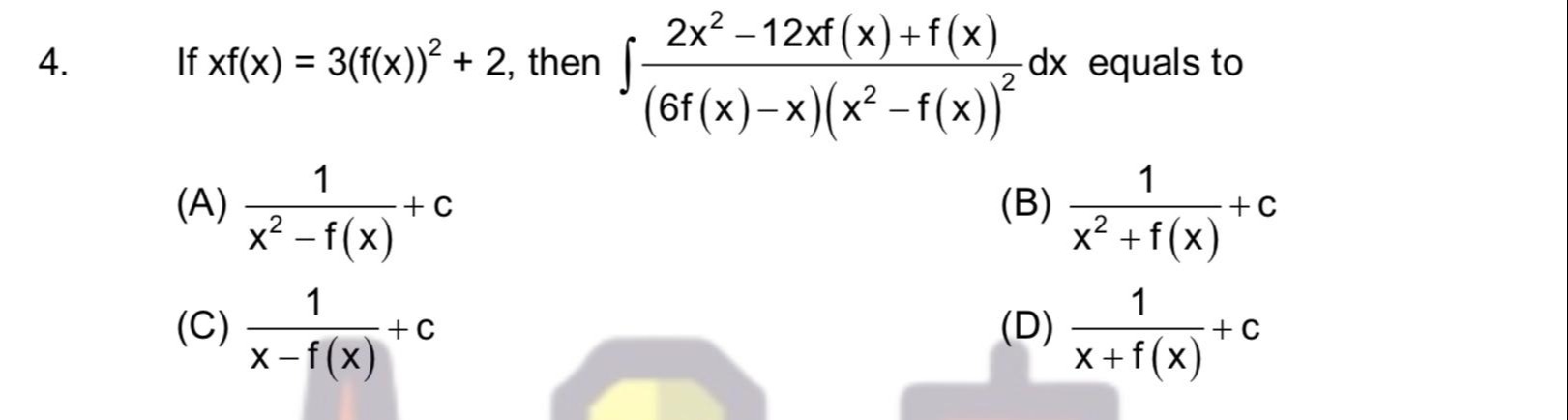
x2−f(x)1+c
x2+f(x)1+c
x−f(x)1+c
x+f(x)1+c
x2−f(x)1+c
Solution
To evaluate the integral, we first analyze the given functional equation and then look for a suitable substitution in the integral.
Given functional equation: xf(x)=3(f(x))2+2
Differentiate both sides with respect to x: Using the product rule on xf(x) and chain rule on 3(f(x))2: dxd(xf(x))=dxd(3(f(x))2+2) 1⋅f(x)+x⋅f′(x)=3⋅2f(x)⋅f′(x)+0 f(x)+xf′(x)=6f(x)f′(x)
Rearrange the terms to find f′(x): f(x)=6f(x)f′(x)−xf′(x) f(x)=(6f(x)−x)f′(x) So, f′(x)=6f(x)−xf(x)
Now consider the integral: I=∫(6f(x)−x)(x2−f(x))22x2−12xf(x)+f(x)dx
Let's look at the term (x2−f(x))2 in the denominator. This suggests a substitution of the form u=x2−f(x).
Let u=x2−f(x). Now, find du by differentiating u with respect to x: du=dxd(x2−f(x))dx du=(2x−f′(x))dx
Substitute the expression for f′(x) we found earlier: du=(2x−6f(x)−xf(x))dx du=(6f(x)−x2x(6f(x)−x)−f(x))dx du=(6f(x)−x12xf(x)−2x2−f(x))dx
Notice that the numerator of the integral is 2x2−12xf(x)+f(x). This is exactly the negative of the numerator in our du expression. So, du=−(6f(x)−x2x2−12xf(x)+f(x))dx This implies that 6f(x)−x2x2−12xf(x)+f(x)dx=−du.
Now, rewrite the integral using our substitution: I=∫(x2−f(x))21⋅(6f(x)−x2x2−12xf(x)+f(x))dx Substitute u=x2−f(x) and (6f(x)−x2x2−12xf(x)+f(x))dx=−du: I=∫u21(−du) I=−∫u−2du
Now, perform the integration: I=−(−2+1u−2+1)+C I=−(−1u−1)+C I=u1+C
Finally, substitute back u=x2−f(x): I=x2−f(x)1+C
Comparing this result with the given options, it matches option (A).
