Solveeit Logo
Login

Question

Question: If $\sin(\theta + \alpha) = a$ & $\sin(\theta + \beta) = b (0 < \alpha, \beta, \theta < \pi/2)$ then...

If sin⁡(θ+α)=a\sin(\theta + \alpha) = a & sin⁡(θ+β)=b(0<α,β,θ<π/2)\sin(\theta + \beta) = b (0 < \alpha, \beta, \theta < \pi/2) then find the value of cos⁡2(α−β)−4abcos⁡(α−β)+sin⁡3x+cos⁡3x=cos⁡32x.\cos^2(\alpha - \beta) - 4ab \cos(\alpha - \beta) + \sin^3 x + \cos^3 x = \cos^3 2x.

Answer

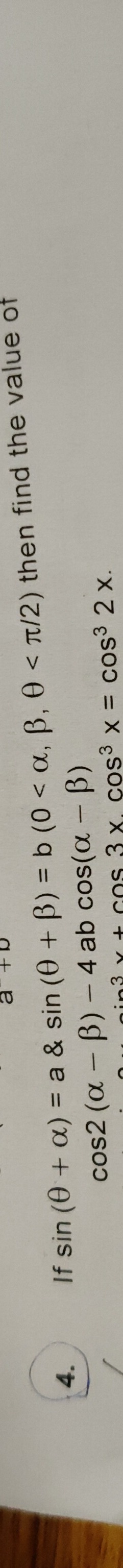
1 - a^2 - b^2 - 2ab \cos(\alpha - \beta)

Explanation

Solution

The problem statement appears to be a combination of two unrelated parts or contains a significant typo.

Part 1: "If sin⁡(θ+α)=a\sin(\theta + \alpha) = a & sin⁡(θ+β)=b(0<α,β,θ<π/2)\sin(\theta + \beta) = b (0 < \alpha, \beta, \theta < \pi/2) then find the value of cos⁡2(α−β)−4abcos⁡(α−β)\cos^2(\alpha - \beta) - 4ab \cos(\alpha - \beta)" Part 2: "+sin⁡3x+cos⁡3x=cos⁡32x.+ \sin^3 x + \cos^3 x = \cos^3 2x." This second part is an equation involving xx and is disconnected from the first part. We will assume the question intends to ask for the value of the expression in Part 1.

Let P=cos⁡(α−β)P = \cos(\alpha - \beta). The expression we need to find is P2−4abPP^2 - 4abP.

We are given:

  1. sin⁡(θ+α)=a\sin(\theta + \alpha) = a
  2. sin⁡(θ+β)=b\sin(\theta + \beta) = b

Since 0<α,β,θ<π/20 < \alpha, \beta, \theta < \pi/2, it implies that 0<θ+α<π0 < \theta + \alpha < \pi and 0<θ+β<π0 < \theta + \beta < \pi. More specifically, since θ,α,β\theta, \alpha, \beta are all acute, θ+α\theta+\alpha and θ+β\theta+\beta are angles in the first or second quadrant. However, the range 0<α,β,θ<π/20 < \alpha, \beta, \theta < \pi/2 implies 0<θ+α<π0 < \theta+\alpha < \pi and 0<θ+β<π0 < \theta+\beta < \pi. Since sin⁡(θ+α)=a\sin(\theta+\alpha)=a and sin⁡(θ+β)=b\sin(\theta+\beta)=b, aa and bb are positive.

Also, cos⁡(θ+α)=±1−a2\cos(\theta + \alpha) = \pm\sqrt{1 - a^2} and cos⁡(θ+β)=±1−b2\cos(\theta + \beta) = \pm\sqrt{1 - b^2}.

Given the context of common trigonometric problems, it's usually assumed that θ+α\theta+\alpha and θ+β\theta+\beta are in the first quadrant, so cos⁡(θ+α)=1−a2\cos(\theta+\alpha) = \sqrt{1 - a^2} and cos⁡(θ+β)=1−b2\cos(\theta+\beta) = \sqrt{1 - b^2}. This is consistent with 0<α,β,θ<π/20 < \alpha, \beta, \theta < \pi/2, which makes θ+α<π\theta+\alpha < \pi and θ+β<π\theta+\beta < \pi.

If θ+α∈(π/2,π)\theta+\alpha \in (\pi/2, \pi), then cos⁡(θ+α)\cos(\theta+\alpha) would be negative. But for these problems, it is usually assumed that α,β,θ\alpha, \beta, \theta are small enough such that θ+α<π/2\theta+\alpha < \pi/2 and θ+β<π/2\theta+\beta < \pi/2. If not, the sign of the cosine terms would depend on the specific values. However, the range 0<α,β,θ<π/20 < \alpha, \beta, \theta < \pi/2 means θ+α\theta+\alpha can be up to π\pi, so cos⁡(θ+α)\cos(\theta+\alpha) could be negative.

Let's consider the identity: cos⁡(X−Y)=cos⁡Xcos⁡Y+sin⁡Xsin⁡Y\cos(X - Y) = \cos X \cos Y + \sin X \sin Y Let X=θ+αX = \theta + \alpha and Y=θ+βY = \theta + \beta. Then X−Y=(θ+α)−(θ+β)=α−βX - Y = (\theta + \alpha) - (\theta + \beta) = \alpha - \beta. So, cos⁡(α−β)=cos⁡(θ+α)cos⁡(θ+β)+sin⁡(θ+α)sin⁡(θ+β)\cos(\alpha - \beta) = \cos(\theta + \alpha) \cos(\theta + \beta) + \sin(\theta + \alpha) \sin(\theta + \beta). Substitute the given values: P=cos⁡(θ+α)cos⁡(θ+β)+abP = \cos(\theta + \alpha) \cos(\theta + \beta) + ab.

Rearrange the equation: P−ab=cos⁡(θ+α)cos⁡(θ+β)P - ab = \cos(\theta + \alpha) \cos(\theta + \beta). Square both sides: (P−ab)2=cos⁡2(θ+α)cos⁡2(θ+β)(P - ab)^2 = \cos^2(\theta + \alpha) \cos^2(\theta + \beta). Using the identity cos⁡2x=1−sin⁡2x\cos^2 x = 1 - \sin^2 x: (P−ab)2=(1−sin⁡2(θ+α))(1−sin⁡2(θ+β))(P - ab)^2 = (1 - \sin^2(\theta + \alpha)) (1 - \sin^2(\theta + \beta)). (P−ab)2=(1−a2)(1−b2)(P - ab)^2 = (1 - a^2)(1 - b^2). Expand both sides: P2−2abP+a2b2=1−b2−a2+a2b2P^2 - 2abP + a^2b^2 = 1 - b^2 - a^2 + a^2b^2. Subtract a2b2a^2b^2 from both sides: P2−2abP=1−a2−b2P^2 - 2abP = 1 - a^2 - b^2.

The expression we need to find is P2−4abPP^2 - 4abP. We can rewrite this as (P2−2abP)−2abP(P^2 - 2abP) - 2abP. Substitute the derived relation P2−2abP=1−a2−b2P^2 - 2abP = 1 - a^2 - b^2: P2−4abP=(1−a2−b2)−2abPP^2 - 4abP = (1 - a^2 - b^2) - 2abP. Substitute P=cos⁡(α−β)P = \cos(\alpha - \beta) back into the expression: Value =1−a2−b2−2abcos⁡(α−β)= 1 - a^2 - b^2 - 2ab \cos(\alpha - \beta).

This is the most simplified form the expression can take using the given information. The problem does not provide enough constraints for the expression to simplify to a numerical constant.

The second part of the question "+sin⁡3x+cos⁡3x=cos⁡32x.+ \sin^3 x + \cos^3 x = \cos^3 2x." is a separate equation and cannot be "found" as a value of the first expression. It is likely a typo or an unrelated question appended.