Solveeit Logo
Login

Question

Question: If $\begin{vmatrix} \sin 3A & \sin 2A & \sin A\\ \sin 3B & \sin 2B & \sin B\\ \sin 3C & \sin 2C & \s...

If ∣sin⁡3Asin⁡2Asin⁡Asin⁡3Bsin⁡2Bsin⁡Bsin⁡3Csin⁡2Csin⁡C∣=λsin⁡Asin⁡Bsin⁡Csin⁡A+B2sin⁡A+C2sin⁡B+C2sin⁡A−B2sin⁡B−C2sin⁡C−A2\begin{vmatrix} \sin 3A & \sin 2A & \sin A\\ \sin 3B & \sin 2B & \sin B\\ \sin 3C & \sin 2C & \sin C \end{vmatrix} = \lambda \sin A \sin B \sin C \sin \frac{A+B}{2} \sin \frac{A+C}{2} \sin \frac{B+C}{2} \sin \frac{A-B}{2} \sin \frac{B-C}{2} \sin \frac{C-A}{2},

then the value of λ\lambda will be-

A

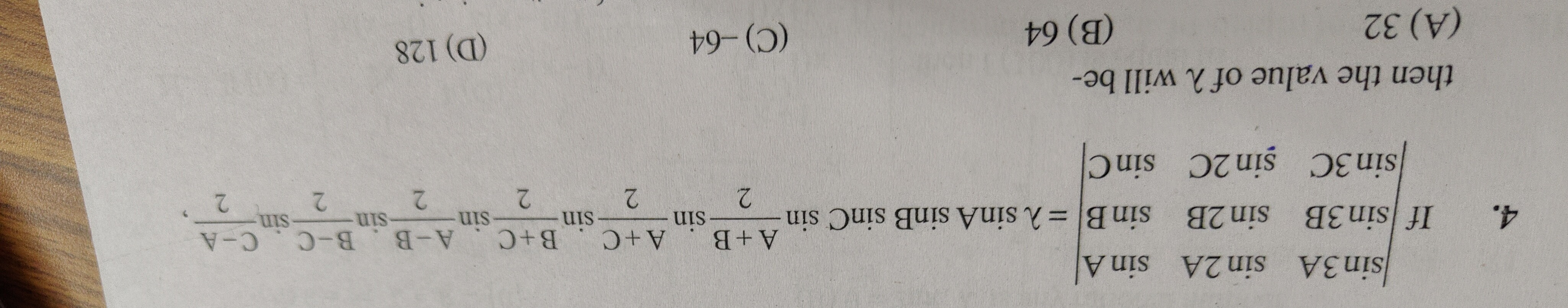
32

B

64

C

-64

D

128

Answer

64

Explanation

Solution

The problem requires us to find the value of λ\lambda by evaluating the given determinant and comparing it with the provided expression.

The given determinant is: D=∣sin⁡3Asin⁡2Asin⁡Asin⁡3Bsin⁡2Bsin⁡Bsin⁡3Csin⁡2Csin⁡C∣D = \begin{vmatrix} \sin 3A & \sin 2A & \sin A\\ \sin 3B & \sin 2B & \sin B\\ \sin 3C & \sin 2C & \sin C \end{vmatrix}

Step 1: Factor out sin⁡A,sin⁡B,sin⁡C\sin A, \sin B, \sin C from rows.

We can take sin⁡A\sin A common from the first row, sin⁡B\sin B from the second row, and sin⁡C\sin C from the third row. D=sin⁡Asin⁡Bsin⁡C∣sin⁡3Asin⁡Asin⁡2Asin⁡A1sin⁡3Bsin⁡Bsin⁡2Bsin⁡B1sin⁡3Csin⁡Csin⁡2Csin⁡C1∣D = \sin A \sin B \sin C \begin{vmatrix} \frac{\sin 3A}{\sin A} & \frac{\sin 2A}{\sin A} & 1\\ \frac{\sin 3B}{\sin B} & \frac{\sin 2B}{\sin B} & 1\\ \frac{\sin 3C}{\sin C} & \frac{\sin 2C}{\sin C} & 1 \end{vmatrix}

Step 2: Apply trigonometric identities.

We use the identities: sin⁡3xsin⁡x=3sin⁡x−4sin⁡3xsin⁡x=3−4sin⁡2x\frac{\sin 3x}{\sin x} = \frac{3 \sin x - 4 \sin^3 x}{\sin x} = 3 - 4 \sin^2 x sin⁡2xsin⁡x=2sin⁡xcos⁡xsin⁡x=2cos⁡x\frac{\sin 2x}{\sin x} = \frac{2 \sin x \cos x}{\sin x} = 2 \cos x

Substitute these into the determinant: D=sin⁡Asin⁡Bsin⁡C∣3−4sin⁡2A2cos⁡A13−4sin⁡2B2cos⁡B13−4sin⁡2C2cos⁡C1∣D = \sin A \sin B \sin C \begin{vmatrix} 3 - 4 \sin^2 A & 2 \cos A & 1\\ 3 - 4 \sin^2 B & 2 \cos B & 1\\ 3 - 4 \sin^2 C & 2 \cos C & 1 \end{vmatrix}

Step 3: Further simplify the first column using sin⁡2x=1−cos⁡2x2\sin^2 x = \frac{1 - \cos 2x}{2}.

3−4sin⁡2x=3−4(1−cos⁡2x2)=3−2(1−cos⁡2x)=3−2+2cos⁡2x=1+2cos⁡2x3 - 4 \sin^2 x = 3 - 4 \left(\frac{1 - \cos 2x}{2}\right) = 3 - 2(1 - \cos 2x) = 3 - 2 + 2 \cos 2x = 1 + 2 \cos 2x.

So the determinant becomes: D=sin⁡Asin⁡Bsin⁡C∣1+2cos⁡2A2cos⁡A11+2cos⁡2B2cos⁡B11+2cos⁡2C2cos⁡C1∣D = \sin A \sin B \sin C \begin{vmatrix} 1 + 2 \cos 2A & 2 \cos A & 1\\ 1 + 2 \cos 2B & 2 \cos B & 1\\ 1 + 2 \cos 2C & 2 \cos C & 1 \end{vmatrix}

Step 4: Apply column operation C1→C1−C3C_1 \to C_1 - C_3.

D=sin⁡Asin⁡Bsin⁡C∣(1+2cos⁡2A)−12cos⁡A1(1+2cos⁡2B)−12cos⁡B1(1+2cos⁡2C)−12cos⁡C1∣D = \sin A \sin B \sin C \begin{vmatrix} (1 + 2 \cos 2A) - 1 & 2 \cos A & 1\\ (1 + 2 \cos 2B) - 1 & 2 \cos B & 1\\ (1 + 2 \cos 2C) - 1 & 2 \cos C & 1 \end{vmatrix} D=sin⁡Asin⁡Bsin⁡C∣2cos⁡2A2cos⁡A12cos⁡2B2cos⁡B12cos⁡2C2cos⁡C1∣D = \sin A \sin B \sin C \begin{vmatrix} 2 \cos 2A & 2 \cos A & 1\\ 2 \cos 2B & 2 \cos B & 1\\ 2 \cos 2C & 2 \cos C & 1 \end{vmatrix}

Step 5: Factor out constants from columns.

Take 2 common from C1C_1 and 2 common from C2C_2. D=sin⁡Asin⁡Bsin⁡C⋅2⋅2∣cos⁡2Acos⁡A1cos⁡2Bcos⁡B1cos⁡2Ccos⁡C1∣D = \sin A \sin B \sin C \cdot 2 \cdot 2 \begin{vmatrix} \cos 2A & \cos A & 1\\ \cos 2B & \cos B & 1\\ \cos 2C & \cos C & 1 \end{vmatrix} D=4sin⁡Asin⁡Bsin⁡C∣cos⁡2Acos⁡A1cos⁡2Bcos⁡B1cos⁡2Ccos⁡C1∣D = 4 \sin A \sin B \sin C \begin{vmatrix} \cos 2A & \cos A & 1\\ \cos 2B & \cos B & 1\\ \cos 2C & \cos C & 1 \end{vmatrix}

Step 6: Apply cos⁡2x=2cos⁡2x−1\cos 2x = 2 \cos^2 x - 1.

D=4sin⁡Asin⁡Bsin⁡C∣2cos⁡2A−1cos⁡A12cos⁡2B−1cos⁡B12cos⁡2C−1cos⁡C1∣D = 4 \sin A \sin B \sin C \begin{vmatrix} 2 \cos^2 A - 1 & \cos A & 1\\ 2 \cos^2 B - 1 & \cos B & 1\\ 2 \cos^2 C - 1 & \cos C & 1 \end{vmatrix}

Step 7: Apply column operation C1→C1+C3C_1 \to C_1 + C_3.

D=4sin⁡Asin⁡Bsin⁡C∣(2cos⁡2A−1)+1cos⁡A1(2cos⁡2B−1)+1cos⁡B1(2cos⁡2C−1)+1cos⁡C1∣D = 4 \sin A \sin B \sin C \begin{vmatrix} (2 \cos^2 A - 1) + 1 & \cos A & 1\\ (2 \cos^2 B - 1) + 1 & \cos B & 1\\ (2 \cos^2 C - 1) + 1 & \cos C & 1 \end{vmatrix} D=4sin⁡Asin⁡Bsin⁡C∣2cos⁡2Acos⁡A12cos⁡2Bcos⁡B12cos⁡2Ccos⁡C1∣D = 4 \sin A \sin B \sin C \begin{vmatrix} 2 \cos^2 A & \cos A & 1\\ 2 \cos^2 B & \cos B & 1\\ 2 \cos^2 C & \cos C & 1 \end{vmatrix}

Step 8: Factor out constant from C1C_1.

Take 2 common from C1C_1. D=4sin⁡Asin⁡Bsin⁡C⋅2∣cos⁡2Acos⁡A1cos⁡2Bcos⁡B1cos⁡2Ccos⁡C1∣D = 4 \sin A \sin B \sin C \cdot 2 \begin{vmatrix} \cos^2 A & \cos A & 1\\ \cos^2 B & \cos B & 1\\ \cos^2 C & \cos C & 1 \end{vmatrix} D=8sin⁡Asin⁡Bsin⁡C∣cos⁡2Acos⁡A1cos⁡2Bcos⁡B1cos⁡2Ccos⁡C1∣D = 8 \sin A \sin B \sin C \begin{vmatrix} \cos^2 A & \cos A & 1\\ \cos^2 B & \cos B & 1\\ \cos^2 C & \cos C & 1 \end{vmatrix}

Step 9: Evaluate the Vandermonde-like determinant.

The determinant ∣x2x1y2y1z2z1∣\begin{vmatrix} x^2 & x & 1 \\ y^2 & y & 1 \\ z^2 & z & 1 \end{vmatrix} evaluates to (x−y)(y−z)(x−z)(x-y)(y-z)(x-z). Here, x=cos⁡Ax = \cos A, y=cos⁡By = \cos B, z=cos⁡Cz = \cos C. So, ∣cos⁡2Acos⁡A1cos⁡2Bcos⁡B1cos⁡2Ccos⁡C1∣=(cos⁡A−cos⁡B)(cos⁡B−cos⁡C)(cos⁡A−cos⁡C)\begin{vmatrix} \cos^2 A & \cos A & 1\\ \cos^2 B & \cos B & 1\\ \cos^2 C & \cos C & 1 \end{vmatrix} = (\cos A - \cos B)(\cos B - \cos C)(\cos A - \cos C).

Substitute this back into the expression for D: D=8sin⁡Asin⁡Bsin⁡C(cos⁡A−cos⁡B)(cos⁡B−cos⁡C)(cos⁡A−cos⁡C)D = 8 \sin A \sin B \sin C (\cos A - \cos B)(\cos B - \cos C)(\cos A - \cos C)

Step 10: Convert differences of cosines into products of sines.

Using the sum-to-product formula cos⁡X−cos⁡Y=−2sin⁡X+Y2sin⁡X−Y2\cos X - \cos Y = -2 \sin \frac{X+Y}{2} \sin \frac{X-Y}{2}: cos⁡A−cos⁡B=−2sin⁡A+B2sin⁡A−B2\cos A - \cos B = -2 \sin \frac{A+B}{2} \sin \frac{A-B}{2} cos⁡B−cos⁡C=−2sin⁡B+C2sin⁡B−C2\cos B - \cos C = -2 \sin \frac{B+C}{2} \sin \frac{B-C}{2} cos⁡A−cos⁡C=−2sin⁡A+C2sin⁡A−C2\cos A - \cos C = -2 \sin \frac{A+C}{2} \sin \frac{A-C}{2}

Substitute these into the expression for D: D=8sin⁡Asin⁡Bsin⁡C(−2sin⁡A+B2sin⁡A−B2)(−2sin⁡B+C2sin⁡B−C2)(−2sin⁡A+C2sin⁡A−C2)D = 8 \sin A \sin B \sin C \left( -2 \sin \frac{A+B}{2} \sin \frac{A-B}{2} \right) \left( -2 \sin \frac{B+C}{2} \sin \frac{B-C}{2} \right) \left( -2 \sin \frac{A+C}{2} \sin \frac{A-C}{2} \right) D=8⋅(−2)3sin⁡Asin⁡Bsin⁡Csin⁡A+B2sin⁡A−B2sin⁡B+C2sin⁡B−C2sin⁡A+C2sin⁡A−C2D = 8 \cdot (-2)^3 \sin A \sin B \sin C \sin \frac{A+B}{2} \sin \frac{A-B}{2} \sin \frac{B+C}{2} \sin \frac{B-C}{2} \sin \frac{A+C}{2} \sin \frac{A-C}{2} D=8⋅(−8)sin⁡Asin⁡Bsin⁡Csin⁡A+B2sin⁡B+C2sin⁡A+C2sin⁡A−B2sin⁡B−C2sin⁡A−C2D = 8 \cdot (-8) \sin A \sin B \sin C \sin \frac{A+B}{2} \sin \frac{B+C}{2} \sin \frac{A+C}{2} \sin \frac{A-B}{2} \sin \frac{B-C}{2} \sin \frac{A-C}{2} D=−64sin⁡Asin⁡Bsin⁡Csin⁡A+B2sin⁡B+C2sin⁡A+C2sin⁡A−B2sin⁡B−C2sin⁡A−C2D = -64 \sin A \sin B \sin C \sin \frac{A+B}{2} \sin \frac{B+C}{2} \sin \frac{A+C}{2} \sin \frac{A-B}{2} \sin \frac{B-C}{2} \sin \frac{A-C}{2}

Step 11: Compare with the given expression.

The given expression for D is: λsin⁡Asin⁡Bsin⁡Csin⁡A+B2sin⁡A+C2sin⁡B+C2sin⁡A−B2sin⁡B−C2sin⁡C−A2\lambda \sin A \sin B \sin C \sin \frac{A+B}{2} \sin \frac{A+C}{2} \sin \frac{B+C}{2} \sin \frac{A-B}{2} \sin \frac{B-C}{2} \sin \frac{C-A}{2}

We have sin⁡A−C2=−sin⁡C−A2\sin \frac{A-C}{2} = -\sin \frac{C-A}{2}. Substitute this into our derived expression for D: D=−64sin⁡Asin⁡Bsin⁡Csin⁡A+B2sin⁡B+C2sin⁡A+C2sin⁡A−B2sin⁡B−C2(−sin⁡C−A2)D = -64 \sin A \sin B \sin C \sin \frac{A+B}{2} \sin \frac{B+C}{2} \sin \frac{A+C}{2} \sin \frac{A-B}{2} \sin \frac{B-C}{2} \left( -\sin \frac{C-A}{2} \right) D=64sin⁡Asin⁡Bsin⁡Csin⁡A+B2sin⁡B+C2sin⁡A+C2sin⁡A−B2sin⁡B−C2sin⁡C−A2D = 64 \sin A \sin B \sin C \sin \frac{A+B}{2} \sin \frac{B+C}{2} \sin \frac{A+C}{2} \sin \frac{A-B}{2} \sin \frac{B-C}{2} \sin \frac{C-A}{2}

Comparing this with the given expression, we find that λ=64\lambda = 64.