Question

If $a_i > 0$ (i = 1, 2, 3, …, n), prove that $\sum_{1 \leq i < j \leq n} \sqrt{a_i a_j} \leq \frac{n-1}{2} (a_1 + a_2 + ... + a_n)$

Answer 1

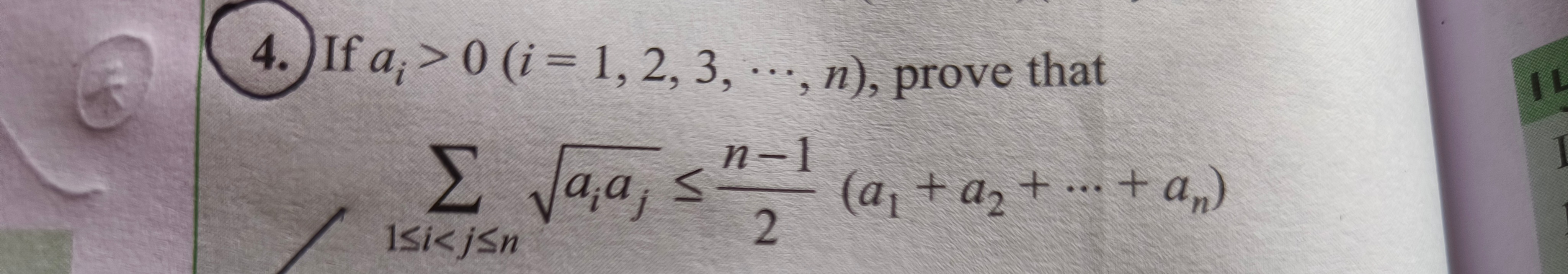
To prove the inequality, we apply the AM-GM inequality to each pair $(a_i, a_j)$, sum over all relevant pairs, simplify the right-hand side, and substitute back into the inequality.

Answer 2

The proof uses the AM-GM inequality, $\sqrt{xy} \leq \frac{x+y}{2}$, applied to each pair $(a_i, a_j)$. Summing these inequalities for all $1 \leq i < j \leq n$ terms, the left side becomes $\sum \sqrt{a_i a_j}$. The right side becomes $\sum \frac{a_i+a_j}{2}$. In the sum $\sum (a_i+a_j)$, each $a_k$ appears exactly $(n-1)$ times, leading to $(n-1)\sum a_k$. This directly yields the desired inequality.

Steps:

1. Apply AM-GM Inequality: $\sqrt{a_i a_j} \leq \frac{a_i + a_j}{2}$

2. Sum over all pairs: $\sum_{1 \leq i < j \leq n} \sqrt{a_i a_j} \leq \sum_{1 \leq i < j \leq n} \frac{a_i + a_j}{2}$

3. Simplify RHS: Analyze how many times each $a_k$ appears in the sum. $a_k$ appears $(n-k)$ times in sums $(a_k + a_j)$ where $j > k$, and $(k-1)$ times in sums $(a_i + a_k)$ where $i < k$. Therefore, $a_k$ appears $(n-1)$ times.

4. Substitute: $\sum_{1 \leq i < j \leq n} \sqrt{a_i a_j} \leq \frac{1}{2} (n-1) (a_1 + a_2 + ... + a_n)$, leading to the desired inequality.