Question

If a, b, c are integers such that $|a - b|^{19} + |c-a|^{19}=1$, find the value of $| c -a | + |a-b| + |b-c|$

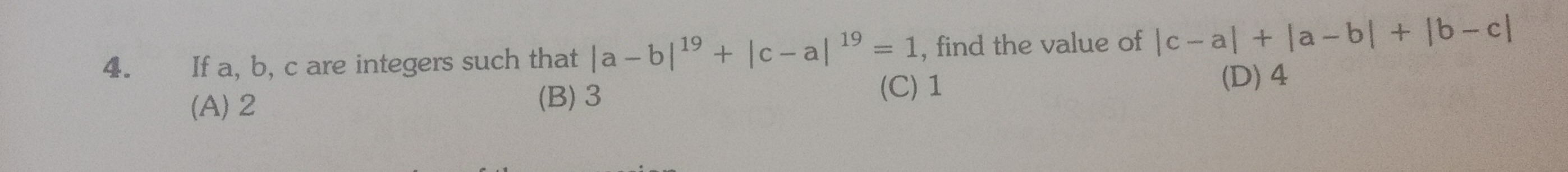
• A. 2
• B. 3
• C. 1
• D. 4

Answer 1

Answer: (A)

2

Answer 2

Let $X = |a - b|$ and $Y = |c - a|$. Since $a, b, c$ are integers, $X$ and $Y$ must be non-negative integers. The given equation is $X^{19} + Y^{19} = 1$. The only non-negative integer solutions are $(X, Y) = (0, 1)$ or $(X, Y) = (1, 0)$. We know that $(a-b) + (b-c) + (c-a) = 0$. Let $u = a-b$ and $w = c-a$. Then $b-c = -(u+w)$. So, $|b-c| = |-(u+w)| = |u+w|$.

Case 1: $|a - b| = 0$ and $|c - a| = 1$. Then $|b-c| = |0 + (c-a)| = |c-a| = 1$. The sum is $|c-a| + |a-b| + |b-c| = 1 + 0 + 1 = 2$.

Case 2: $|a - b| = 1$ and $|c - a| = 0$. Then $|b-c| = |(a-b) + 0| = |a-b| = 1$. The sum is $|c-a| + |a-b| + |b-c| = 0 + 1 + 1 = 2$. In both cases, the sum is 2.