Solveeit Logo
Login

Question

Question: $f(x) = sec^{-1}(sin^{-1}x)$ ...

f(x)=sec−1(sin−1x)f(x) = sec^{-1}(sin^{-1}x)

Answer

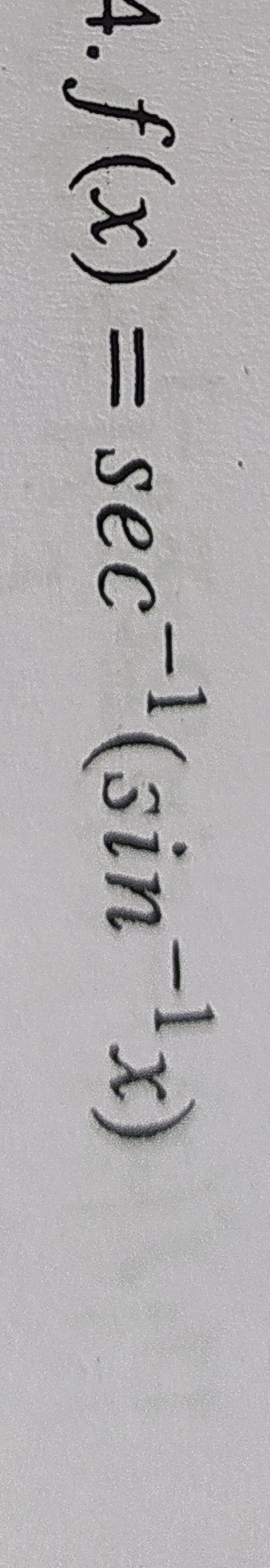
[−1,−sin⁡(1)]∪[sin⁡(1),1][-1, -\sin(1)] \cup [\sin(1), 1]

Explanation

Solution

The given function is f(x)=sec⁡−1(sin⁡−1x)f(x) = \sec^{-1}(\sin^{-1}x).

For the function f(x)f(x) to be defined, two conditions must be met:

  1. The argument of the inner function, sin⁡−1x\sin^{-1}x, must be within its domain. The domain of sin⁡−1x\sin^{-1}x is [−1,1][-1, 1]. Thus, we must have x∈[−1,1]x \in [-1, 1].
  2. The argument of the outer function, sec⁡−1u\sec^{-1}u, where u=sin⁡−1xu = \sin^{-1}x, must be within its domain. The domain of sec⁡−1u\sec^{-1}u is (−∞,−1]∪[1,∞)(-\infty, -1] \cup [1, \infty). Thus, we must have sin⁡−1x∈(−∞,−1]∪[1,∞)\sin^{-1}x \in (-\infty, -1] \cup [1, \infty).

We need to find the values of xx that satisfy both conditions.

Consider the second condition: sin⁡−1x∈(−∞,−1]∪[1,∞)\sin^{-1}x \in (-\infty, -1] \cup [1, \infty). The principal range of the function sin⁡−1x\sin^{-1}x is [−π2,π2][-\frac{\pi}{2}, \frac{\pi}{2}]. We need the values of sin⁡−1x\sin^{-1}x that are in the set (−∞,−1]∪[1,∞)(-\infty, -1] \cup [1, \infty) and also in the range [−π2,π2][-\frac{\pi}{2}, \frac{\pi}{2}]. The intersection of these two sets is [−π2,−1]∪[1,π2][-\frac{\pi}{2}, -1] \cup [1, \frac{\pi}{2}]. So, the second condition is equivalent to sin⁡−1x∈[−π2,−1]∪[1,π2]\sin^{-1}x \in [-\frac{\pi}{2}, -1] \cup [1, \frac{\pi}{2}]. This means either −π2≤sin⁡−1x≤−1-\frac{\pi}{2} \le \sin^{-1}x \le -1 or 1≤sin⁡−1x≤π21 \le \sin^{-1}x \le \frac{\pi}{2}.

Case 1: −π2≤sin⁡−1x≤−1-\frac{\pi}{2} \le \sin^{-1}x \le -1. Since the sine function is strictly increasing on the interval [−π2,π2][-\frac{\pi}{2}, \frac{\pi}{2}], we can apply the sine function to the inequality while preserving the order: sin⁡(−π2)≤sin⁡(sin⁡−1x)≤sin⁡(−1)\sin(-\frac{\pi}{2}) \le \sin(\sin^{-1}x) \le \sin(-1) −1≤x≤sin⁡(−1)-1 \le x \le \sin(-1) Since sin⁡(−1)=−sin⁡(1)\sin(-1) = -\sin(1), this inequality is −1≤x≤−sin⁡(1)-1 \le x \le -\sin(1).

Case 2: 1≤sin⁡−1x≤π21 \le \sin^{-1}x \le \frac{\pi}{2}. Since the sine function is strictly increasing on the interval [−π2,π2][-\frac{\pi}{2}, \frac{\pi}{2}], we can apply the sine function to the inequality while preserving the order: sin⁡(1)≤sin⁡(sin⁡−1x)≤sin⁡(π2)\sin(1) \le \sin(\sin^{-1}x) \le \sin(\frac{\pi}{2}) sin⁡(1)≤x≤1\sin(1) \le x \le 1.

Combining Case 1 and Case 2, the second condition is satisfied when x∈[−1,−sin⁡(1)]∪[sin⁡(1),1]x \in [-1, -\sin(1)] \cup [\sin(1), 1].

Now we must satisfy both conditions:

  1. x∈[−1,1]x \in [-1, 1]
  2. x∈[−1,−sin⁡(1)]∪[sin⁡(1),1]x \in [-1, -\sin(1)] \cup [\sin(1), 1]

The domain of f(x)f(x) is the intersection of these two sets. Since 0<1<π20 < 1 < \frac{\pi}{2}, we have 0<sin⁡(1)<10 < \sin(1) < 1. This implies −1<−sin⁡(1)<0-1 < -\sin(1) < 0. So, the interval [−1,−sin⁡(1)][-1, -\sin(1)] is a subset of [−1,1][-1, 1]. The interval [sin⁡(1),1][\sin(1), 1] is a subset of [−1,1][-1, 1]. Therefore, the set [−1,−sin⁡(1)]∪[sin⁡(1),1][-1, -\sin(1)] \cup [\sin(1), 1] is a subset of [−1,1][-1, 1]. The intersection of [−1,1][-1, 1] and [−1,−sin⁡(1)]∪[sin⁡(1),1][-1, -\sin(1)] \cup [\sin(1), 1] is [−1,−sin⁡(1)]∪[sin⁡(1),1][-1, -\sin(1)] \cup [\sin(1), 1].

Thus, the domain of the function f(x)=sec⁡−1(sin⁡−1x)f(x) = \sec^{-1}(\sin^{-1}x) is [−1,−sin⁡(1)]∪[sin⁡(1),1][-1, -\sin(1)] \cup [\sin(1), 1].