Question
Question: $\frac{dy}{dx} = (x^3 - 2x \tan^{-1}y)(1+y^2)$...
dxdy=(x3−2xtan−1y)(1+y2)
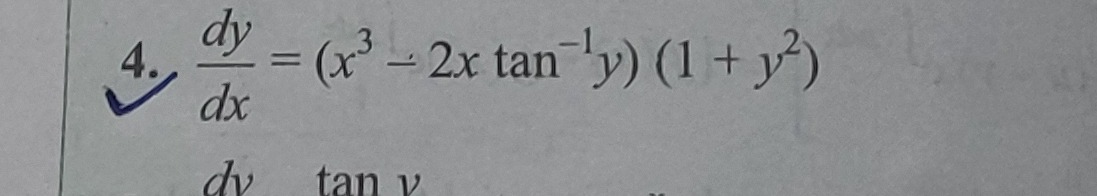
tan−1y=21(x2−1)+Ce−x2
Solution
The given differential equation is: dxdy=(x3−2xtan−1y)(1+y2)
First, rearrange the equation to isolate terms involving y and dy: 1+y21dxdy=x3−2xtan−1y
This form suggests a substitution. Let v=tan−1y. Differentiating v with respect to x using the chain rule: dxdv=dydv⋅dxdy Since v=tan−1y, dydv=1+y21. So, dxdv=1+y21dxdy.
Substitute v and dxdv into the rearranged differential equation: dxdv=x3−2xv
Rearrange this into the standard form of a first-order linear differential equation, which is dxdv+P(x)v=Q(x): dxdv+(2x)v=x3 Here, P(x)=2x and Q(x)=x3.
To solve this linear differential equation, we find the integrating factor (IF): IF=e∫P(x)dx=e∫2xdx=ex2
The general solution for a linear differential equation is given by: v⋅(IF)=∫Q(x)⋅(IF)dx+C Substituting the values: v⋅ex2=∫x3⋅ex2dx+C
Now, we need to evaluate the integral ∫x3ex2dx. Let t=x2. Then dt=2xdx, which means xdx=21dt. The integral becomes: ∫x2⋅ex2⋅xdx=∫t⋅et⋅21dt=21∫tetdt Use integration by parts for ∫tetdt. Let u=t and dv=etdt. Then du=dt and v=et. ∫tetdt=tet−∫etdt=tet−et=et(t−1) Substitute this back: 21∫tetdt=21et(t−1) Now, substitute back t=x2: 21ex2(x2−1)
Substitute this result back into the general solution equation: v⋅ex2=21ex2(x2−1)+C Divide both sides by ex2 (since ex2=0): v=21(x2−1)+Ce−x2
Finally, substitute back v=tan−1y: tan−1y=21(x2−1)+Ce−x2
This is the general solution to the given differential equation.
Explanation of the solution:
The given differential equation is transformed into a first-order linear differential equation by substituting v=tan−1y. This substitution simplifies the left side of the equation from 1+y21dxdy to dxdv. The resulting linear equation dxdv+2xv=x3 is then solved using the integrating factor method. The integrating factor is e∫2xdx=ex2. The solution is v⋅ex2=∫x3ex2dx+C. The integral ∫x3ex2dx is evaluated using substitution (t=x2) followed by integration by parts, yielding 21ex2(x2−1). Substituting this back and solving for v, and then replacing v with tan−1y, gives the final solution tan−1y=21(x2−1)+Ce−x2.
