Question

f:R $\to$ R, f(x) = $\frac{3x^2 + mx + n}{x^2 + 1}$. If the range of this function is [-4, 3), then find the value of $m^2 + n^2$.

Answer 1

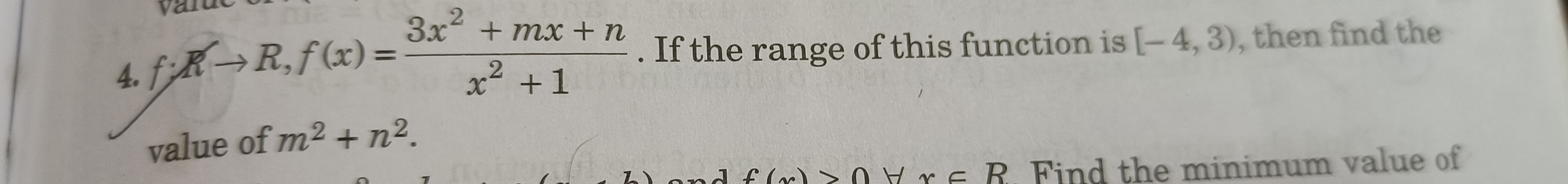
16

Answer 2

Let the given function be $y = f(x) = \frac{3x^2 + mx + n}{x^2 + 1}$. Rearranging the equation to form a quadratic in $x$: $y(x^2 + 1) = 3x^2 + mx + n$ $yx^2 + y = 3x^2 + mx + n$ $(y-3)x^2 - mx + (y-n) = 0$

For real solutions of $x$, the discriminant of this quadratic equation must be non-negative, provided $y \neq 3$.

Case 1: $y \neq 3$ The discriminant $D = (-m)^2 - 4(y-3)(y-n) \ge 0$. $m^2 - 4(y^2 - ny - 3y + 3n) \ge 0$ $m^2 - 4y^2 + 4ny + 12y - 12n \ge 0$ Rearranging into a quadratic inequality in $y$: $4y^2 - (4n+12)y - (m^2 - 12n) \le 0$

Since the range of the function is $[-4, 3)$, the quadratic $4y^2 - (4n+12)y - (m^2 - 12n)$ must be less than or equal to zero for $y$ values between $-4$ and $3$. This means the roots of $4y^2 - (4n+12)y - (m^2 - 12n) = 0$ are $-4$ and $3$.

We can write the quadratic in terms of its roots: $4(y - (-4))(y - 3) = 4(y+4)(y-3) = 4(y^2 + y - 12) = 4y^2 + 4y - 48$.

Equating the coefficients of $4y^2 - (4n+12)y - (m^2 - 12n)$ and $4y^2 + 4y - 48$:

1. Coefficient of $y$: $-(4n+12) = 4 \implies 4n+12 = -4 \implies 4n = -16 \implies n = -4$.
2. Constant term: $-(m^2 - 12n) = -48 \implies m^2 - 12n = 48$. Substitute $n=-4$: $m^2 - 12(-4) = 48 \implies m^2 + 48 = 48 \implies m^2 = 0 \implies m = 0$.

Case 2: $y = 3$ If $y=3$, the equation $(y-3)x^2 - mx + (y-n) = 0$ becomes: $0x^2 - mx + (3-n) = 0 \implies -mx + (3-n) = 0$. For $y=3$ not to be in the range, this equation must not have a real solution for $x$. If $m \neq 0$, then $x = \frac{3-n}{m}$ is a real solution, which means $y=3$ would be in the range, contradicting the given range. Therefore, $m$ must be $0$. If $m=0$, the equation becomes $3-n = 0$, so $n=3$. If $m=0$ and $n=3$, the function is $f(x) = \frac{3x^2+3}{x^2+1} = 3$, so the range is $\{3\}$, which contradicts the given range $[-4, 3)$.

Thus, the values obtained from Case 1 ($m=0, n=-4$) are correct. We need to find $m^2 + n^2$. $m^2 + n^2 = (0)^2 + (-4)^2 = 0 + 16 = 16$.