Question
Question: For three simple statements p, q, and r, $p \rightarrow (q \lor r)$ is logically equivalent to...
For three simple statements p, q, and r, p→(q∨r) is logically equivalent to
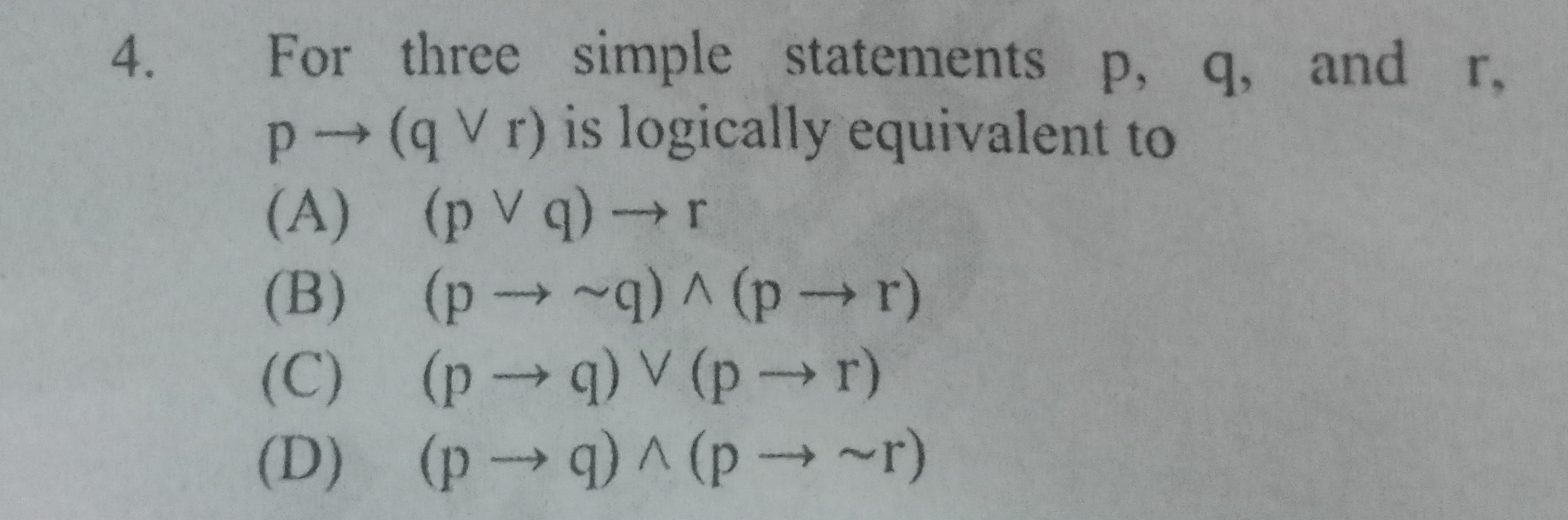
(p∨q)→r
(p→∼q)∧(p→r)
(p→q)∨(p→r)
(p→q)∧(p→∼r)
(C)
Solution
To find the logical equivalent of the statement p→(q∨r), we can transform the statement using standard logical equivalences. The key equivalence is A→B≡∼A∨B.
Applying this equivalence to the given statement: p→(q∨r)≡∼p∨(q∨r) Using the associative property of disjunction (∨), we can write this as: ≡∼p∨q∨r
Now, we examine each option and transform it into a similar form using ∼ and ∨ to check for equivalence.
(A) (p∨q)→r Using A→B≡∼A∨B: (p∨q)→r≡∼(p∨q)∨r Using De Morgan's Law, ∼(A∨B)≡∼A∧∼B: ≡(∼p∧∼q)∨r This is not equivalent to ∼p∨q∨r.
(B) (p→∼q)∧(p→r) Using A→B≡∼A∨B for both implications: (p→∼q)∧(p→r)≡(∼p∨∼q)∧(∼p∨r) Using the distributive property (A∨B)∧(A∨C)≡A∨(B∧C): ≡∼p∨(∼q∧r) This is not equivalent to ∼p∨q∨r.
(C) (p→q)∨(p→r) Using A→B≡∼A∨B for both implications: (p→q)∨(p→r)≡(∼p∨q)∨(∼p∨r) Using the associative and commutative properties of disjunction: ≡∼p∨q∨∼p∨r ≡(∼p∨∼p)∨q∨r Using the idempotent property A∨A≡A: ≡∼p∨q∨r This is equivalent to the original statement.
(D) (p→q)∧(p→∼r) Using A→B≡∼A∨B for both implications: (p→q)∧(p→∼r)≡(∼p∨q)∧(∼p∨∼r) Using the distributive property (A∨B)∧(A∨C)≡A∨(B∧C): ≡∼p∨(q∧∼r) This is not equivalent to ∼p∨q∨r.
Comparing the simplified forms, only option (C) is logically equivalent to the original statement.
