Question

For a real gas (mol. mass = 30) if density at critical point is 0.40 g/cm³ and its T$\_c$ = $\frac{10^4}{41}$K, then calculate Van der Waals constant a (in atm L$^2$mol$^{-2}$).

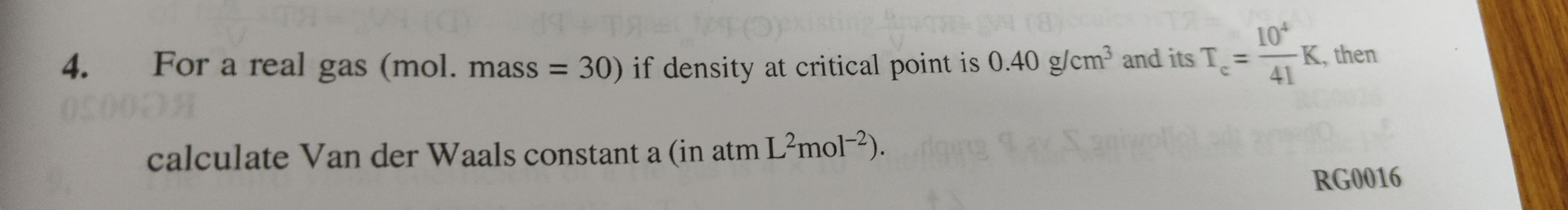
Answer 1

0.633 atm L²mol⁻²

Answer 2

The relationship between the Van der Waals constant 'a' and the critical parameters is given by: $a = \frac{27 R T_c M}{64 \rho_c}$ Where:

• R is the universal gas constant (0.0821 L atm K⁻¹ mol⁻¹)
• $T_c$ is the critical temperature ($\frac{10^4}{41}$ K)
• M is the molar mass (30 g/mol)
• $\rho_c$ is the critical density (0.40 g/cm³ = 400 g/L)

Substituting the values: $a = \frac{27 \times (0.0821 \text{ L atm K⁻¹ mol⁻¹}) \times (\frac{10^4}{41} \text{ K}) \times (30 \text{ g/mol})}{64 \times (400 \text{ g/L})}$ $a = \frac{27 \times 0.0821 \times 10000 \times 30}{41 \times 64 \times 400}$ $a \approx 0.633 \text{ atm L}^2\text{mol}^{-2}$