Question

Find the volume of the solid cut from the square column $|x| + |y| \leq 1$ by the planes z = 0 and 3x + z = 3.

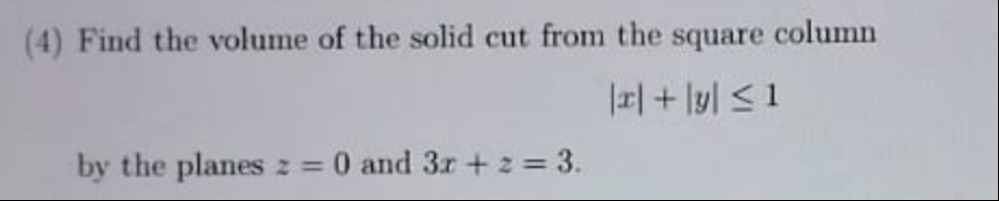
Answer 1

6

Answer 2

The volume $V$ is given by the integral of the height function $z$ over the base region $R$. The base region $R$ is defined by $|x| + |y| \leq 1$. The solid is bounded below by $z=0$ and above by the plane $z = 3 - 3x$.

The volume integral is: $V = \iint_R (z_{upper} - z_{lower}) \,dA = \iint_{|x| + |y| \leq 1} (3 - 3x) \,dA$

This can be split into: $V = \iint_{|x| + |y| \leq 1} 3 \,dA - \iint_{|x| + |y| \leq 1} 3x \,dA$

The first integral is $3$ times the area of the square $|x| + |y| \leq 1$, which is 2. So, $3 \times 2 = 6$. The second integral is 0 because the region $R$ is symmetric about the y-axis and the integrand $x$ is an odd function of $x$.

Thus, $V = 6 - 0 = 6$.