Question
Question: Find the equation to the circle which touches the axis of: (a) x at a distance +3 from the origin a...
Find the equation to the circle which touches the axis of:
(a) x at a distance +3 from the origin and intercepts a distance 6 on the axis of y.
(b) x, pass through the point (1, 1) and have line x + y = 3 as diameter.
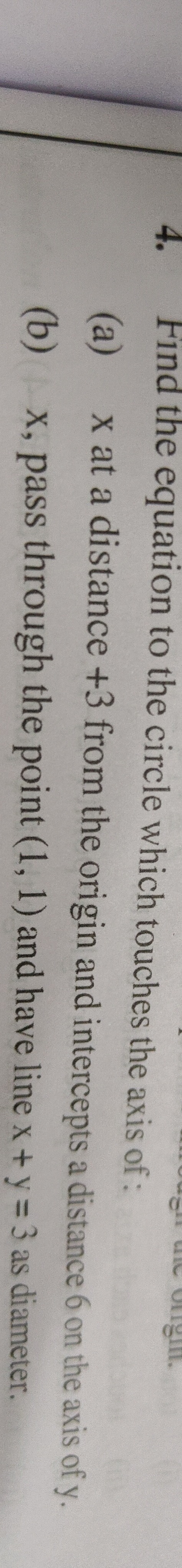
(a) (x−3)2+(y−32)2=18 and (x−3)2+(y+32)2=18
(b) x2+y2−3x−3y+4=0
(a) (x−3)2+(y−3)2=9
(b) x2+y2−2x−2y+1=0
The equations of the circles for part (a) are (x−3)2+(y−32)2=18 and (x−3)2+(y+32)2=18. The equation of the circle for part (b) is x2+y2−3x−3y+4=0.
Solution
(a) Touches x-axis at (3, 0) and intercepts 6 on y-axis:
Let the circle's equation be (x−h)2+(y−k)2=r2. Since it touches the x-axis at (3, 0), the center is (3,k) and the radius is r=∣k∣. The equation becomes (x−3)2+(y−k)2=k2.
When x=0 (y-axis), we have: (0−3)2+(y−k)2=k2 9+y2−2ky+k2=k2 y2−2ky+9=0
The roots y1,y2 of this quadratic give the y-intercepts. The distance between them is ∣y1−y2∣=6. We know that (y1−y2)2=(y1+y2)2−4y1y2. From the quadratic equation, y1+y2=2k and y1y2=9. So, 62=(2k)2−4(9) 36=4k2−36 72=4k2 k2=18 k=±18=±32.
The radius squared is r2=k2=18. The two possible centers are (3,32) and (3,−32). The equations are: (x−3)2+(y−32)2=18 (x−3)2+(y+32)2=18
(b) Passes through (1, 1) and has x + y = 3 as diameter:
If x+y=3 is the diameter, the center (h,k) lies on this line, so h+k=3⟹k=3−h. The radius squared r2 is the square of the distance from the center (h,k) to the point (1,1): r2=(h−1)2+(k−1)2 r2=(h−1)2+(3−h−1)2=(h−1)2+(2−h)2 r2=(h2−2h+1)+(4−4h+h2)=2h2−6h+5.
The equation of the circle is (x−h)2+(y−k)2=r2. Substituting k=3−h and r2=2h2−6h+5: (x−h)2+(y−(3−h))2=2h2−6h+5 x2−2hx+h2+y2−2(3−h)y+(3−h)2=2h2−6h+5 x2−2hx+h2+y2−6y+2hy+9−6h+h2=2h2−6h+5 x2+y2−2hx+2hy−6y+4=0 (x2+y2−6y+4)+2h(y−x)=0.
This is a family of circles. For a unique circle, we consider the case where the point (1,1) is the closest point on the circle to the diameter. This occurs when the radius is minimized. The minimum radius occurs at h=−(−6)/(2×2)=3/2. If h=3/2, then k=3−3/2=3/2. The center is (3/2,3/2). The minimum r2=2(3/2)2−6(3/2)+5=2(9/4)−9+5=9/2−4=1/2. The equation is (x−3/2)2+(y−3/2)2=1/2. x2−3x+9/4+y2−3y+9/4=1/2 x2+y2−3x−3y+18/4=1/2 x2+y2−3x−3y+9/2=1/2 x2+y2−3x−3y+4=0.
