Question
Question: Find smaller area enclosed by $\frac{(x-p)^2}{a^2} + \frac{(x-q)^2}{b^2} = 1$ and $\frac{x-p}{a} + \...
Find smaller area enclosed by a2(x−p)2+b2(x−q)2=1 and ax−p+bx−q=1.
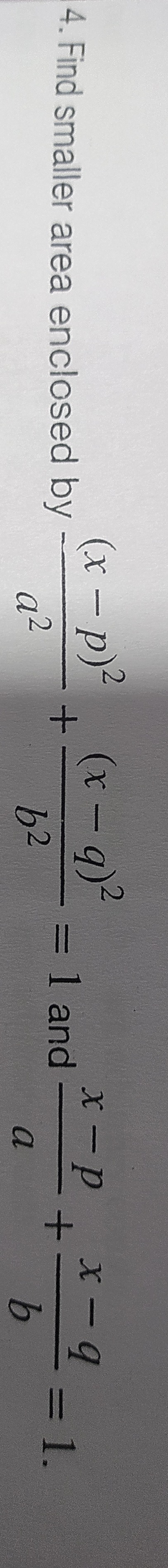
4ab(π−2)
Solution
The problem as stated contains a likely typo. The equations given are:
- a2(x−p)2+b2(x−q)2=1
- ax−p+bx−q=1
If interpreted literally, both equations involve only the variable 'x'. The first equation simplifies to a quadratic equation in 'x': (a21+b21)x2−2(a2p+b2q)x+(a2p2+b2q2−1)=0. This equation would yield at most two values for 'x', representing vertical lines (e.g., x=x1 and x=x2). The second equation also simplifies to a single value for 'x': (a1+b1)x=1+ap+bq⟹x=a+bab+pb+qa. This represents a single vertical line (e.g., x=x0). Three parallel vertical lines (or fewer, if solutions coincide or are complex) do not enclose a finite area in a 2D plane.
Given the context of "applications of integrals" and the structure of the similar question, it is highly probable that the question intends to define an ellipse and a line in the xy-plane. We assume the typo is that (x−q)2 should be (y−q)2 and (x−q)/b should be (y−q)/b.
Let's assume the corrected equations are:
- a2(x−p)2+b2(y−q)2=1 (Equation of an ellipse centered at (p,q))
- ax−p+by−q=1 (Equation of a line)
To solve this, we can use a coordinate transformation. Let X=x−p and Y=y−q. Substituting these into the equations, we get:
- a2X2+b2Y2=1 (Standard equation of an ellipse centered at the origin)
- aX+bY=1 (Equation of a line)
This transformed problem is identical to the similar question provided. The area of a region is invariant under translation of the coordinate system.
The line aX+bY=1 intersects the X-axis at (a,0) and the Y-axis at (0,b). These are also the points where the ellipse intersects the positive X and Y axes. The smaller area enclosed by the ellipse and the line is the area of the segment cut off by the line. This segment lies in the first quadrant of the (X,Y) coordinate system.
The area of the quarter ellipse in the first quadrant is 41πab. The line aX+bY=1 forms a right-angled triangle with the X and Y axes in the first quadrant. The area of this triangle is 21×base×height=21×a×b=2ab.
The smaller area enclosed by the ellipse and the line is the area of the quarter ellipse minus the area of this triangle. Area = Area(Quarter Ellipse) - Area(Triangle) Area = 41πab−21ab Area = ab(4π−21) Area = 4ab(π−2)
This result can also be obtained by integration: The upper half of the ellipse is given by Y=b1−a2X2. The line is given by Y=b(1−aX). The intersection points are (0,b) and (a,0). The area is given by the integral of the difference between the ellipse's Y-coordinate and the line's Y-coordinate from X=0 to X=a: Area =∫0a(b1−a2X2−b(1−aX))dX Area =ab∫0aa2−X2dX−ab∫0a(a−X)dX The first integral: ab[2Xa2−X2+2a2sin−1(aX)]0a=ab(2a2sin−1(1)−0)=ab2a22π=4πab. The second integral: −ab[aX−2X2]0a=−ab(a2−2a2)=−ab2a2=−2ab. Total Area =4πab−2ab=4ab(π−2).
The final answer is 4ab(π−2).
Explanation of the solution: The given equations are interpreted as an ellipse a2(x−p)2+b2(y−q)2=1 and a line ax−p+by−q=1, assuming a typo in the original question. A coordinate transformation X=x−p and Y=y−q simplifies the problem to finding the area enclosed by the standard ellipse a2X2+b2Y2=1 and the line aX+bY=1. The line intersects the ellipse at (a,0) and (0,b) in the new coordinate system. The smaller area is the segment of the ellipse in the first quadrant cut by this line. This area is found by subtracting the area of the triangle formed by the line and the axes (21ab) from the area of the quarter ellipse (41πab). The result is 4ab(π−2).
