Question

Copper reduces HNO3 into NO2 depending upon concentration of HNO3 in solution. Assume of the follo [Cu(NO3)2] = 0.1M and PNO₂ = 10⁻³ bar, at which concentration of HNO3, thermodynamic tendency ect. reduction of HNO3 into NO2 by copper is feasible? [Given E°Cu²⁺|Cu = +0.34 volt, E°HNO₃|NO₂ = +0.79 volt]

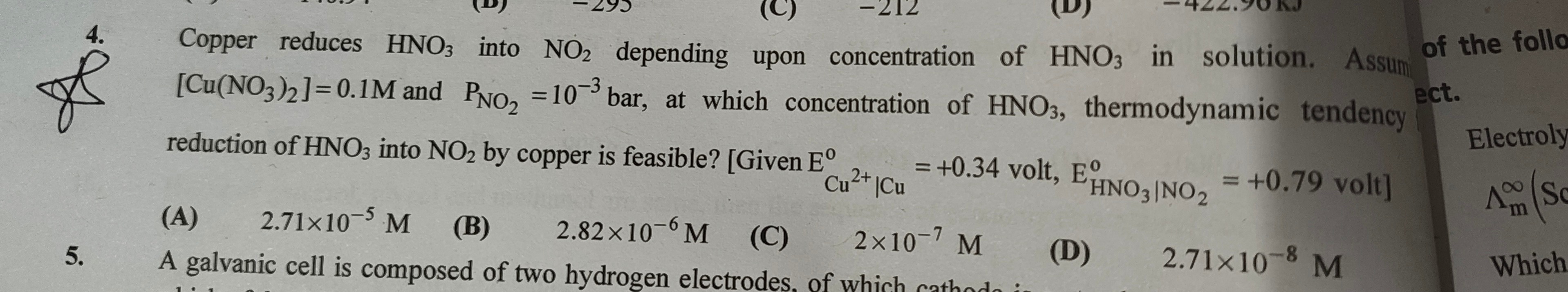
• A. 2.71×10⁻⁵ M
• B. 2.82×10⁻⁶ M
• C. 2×10⁻⁷ M
• D. 2.71×10⁻⁸ M

Answer 1

Answer: (B)

2.82×10⁻⁶ M

Answer 2

Solution:

1. Write the overall reaction:
     Cu(s) + 4 HNO₃ → Cu(NO₃)₂ + 2 NO₂ + 2 H₂O

2. Identify half‐reactions and standard potentials:
    – Oxidation (copper): Cu(s) → Cu²⁺ + 2e⁻   E°₍red₎ = +0.34 V
    – Reduction (nitric acid to NO₂): (given E° = +0.79 V)

3. Determine the standard cell potential:
     E°₍cell₎ = E°₍cathode₎ − E°₍anode₎ = (+0.79 V) − (+0.34 V) = +0.45 V

4. Write the reaction quotient Q:
    Assuming activity of water = 1 and using the given concentrations/pressures,
     Q = ([Cu(NO₃)₂]·(P₍NO₂₎)²) / ([HNO₃]⁴)
    Given: [Cu(NO₃)₂] = 0.1 M and P₍NO₂₎ = 10⁻³ bar.

5. Apply the Nernst equation at equilibrium (E₍cell₎ = 0 for borderline feasibility):
     0 = E°₍cell₎ − (0.0592/2)·log₁₀Q
     ⇒ log₁₀Q = (2·0.45)/0.0592 ≈ 15.20
     ⇒ Q ≈ 10^(15.20) ≈ 1.6×10¹⁵

6. Solve for [HNO₃]:
    Since Q = (0.1 × (10⁻³)²) / ([HNO₃]⁴), we have
     [HNO₃]⁴ = (0.1 × 10⁻⁶) / (1.6×10¹⁵) = 10⁻⁷/(1.6×10¹⁵) ≈ 6.25×10⁻²³
    Taking the fourth root:
     [HNO₃] = (6.25×10⁻²³)^(1/4) ≈ 1.58×10^(–23/4)
    Since (–23/4) ≈ –5.75,
     [HNO₃] ≈ 1.58 × 10⁻⁵.75 ≈ 1.58 × 1.78×10⁻⁶ ≈ 2.82×10⁻⁶ M

Answer:
Option (B) 2.82×10⁻⁶ M

---

Brief Explanation:
For the reaction Cu + 4 HNO₃ → Cu(NO₃)₂ + 2 NO₂ + 2 H₂O, the overall standard EMF is +0.45 V. Setting the actual cell potential to zero (borderline spontaneity), we use the Nernst equation to relate the reaction quotient Q = (Cu(NO₃)₂²)/[HNO₃]⁴. With the given [Cu(NO₃)₂] and P₍NO₂₎, solving for [HNO₃] gives approximately 2.82×10⁻⁶ M.