Question
Question: Determine whether the series converges or diverges: $\sum_{n=3}^{\infty} \frac{7}{\sqrt{n+1} \ln(\s...
Determine whether the series converges or diverges:
∑n=3∞n+1ln(n+1)7
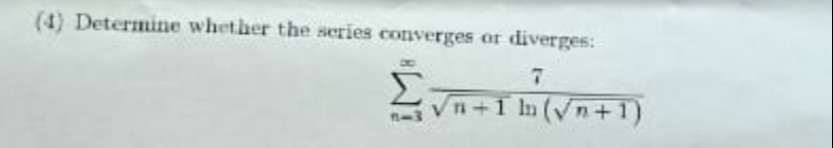
Diverges
Solution
To determine whether the series ∑n=3∞n+1ln(n+1)7 converges or diverges, we can use the Limit Comparison Test.
Let an=n+1ln(n+1)7. We can rewrite ln(n+1) as 21ln(n+1), so an=n+1ln(n+1)14.
For large n, n+1≈n and ln(n+1)≈lnn. Thus, an≈nlnn14.
Consider the series ∑n=2∞np(lnn)q1. This series diverges if p≤1 and q≤1. In our case, we have an≈n1/2(lnn)114, where p=1/2<1 and q=1.
Let's use the Limit Comparison Test with bn=nlnn1. We know that ∑n=2∞nlnn1 diverges because p=1/2<1.
Now, let's compute the limit:
L=limn→∞bnan=limn→∞nlnn1n+1ln(n+1)14=limn→∞n+1ln(n+1)14nlnn=limn→∞14n+1n⋅ln(n+1)lnn
We know limn→∞n+1n=limn→∞1+1/n1=1=1.
We also know limn→∞ln(n+1)lnn=limn→∞ln(n(1+1/n))lnn=limn→∞lnn+ln(1+1/n)lnn=limn→∞1+lnnln(1+1/n)1=1+01=1.
So, L=14⋅1⋅1=14.
Since L=14 (a finite, positive number) and ∑bn=∑nlnn1 diverges, by the Limit Comparison Test, the series ∑an also diverges.
Therefore, the series diverges.
