Question

Three mutually tangent circles of equal radius 2 are as shown in the figure. The area of shaded portion is -

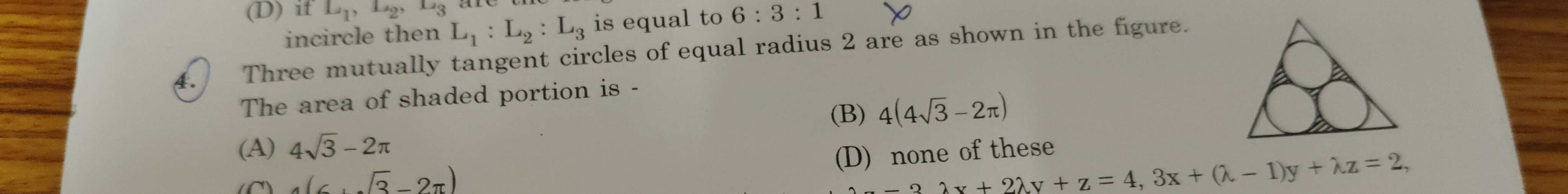
• A. $4\sqrt{3}-2\pi$
• B. $4(4\sqrt{3}-2\pi)$
• C. none of these

Answer 1

Answer: (A)

The area of the shaded portion is $4\sqrt{3}-2\pi$.

Answer 2

The problem asks for the area of the shaded region. The figure shows three mutually tangent circles of equal radius 2. The shaded region is the area enclosed by these three circles.

1. Identify the geometry: When three identical circles are mutually tangent, their centers form an equilateral triangle.
2. Calculate the side length of the triangle formed by centers: Since the radius of each circle is $r=2$, the distance between the centers of any two tangent circles is $2r = 2 \times 2 = 4$. So, the triangle formed by the centers is an equilateral triangle with side length 4.
3. Calculate the area of this equilateral triangle: The area of an equilateral triangle with side $a$ is $\frac{\sqrt{3}}{4}a^2$. For this triangle, $a=4$, so its area is $\frac{\sqrt{3}}{4}(4^2) = \frac{\sqrt{3}}{4} \times 16 = 4\sqrt{3}$.
4. Calculate the area of the circular sectors within the triangle: Each vertex of the equilateral triangle formed by the centers corresponds to the center of a circle. The angle of an equilateral triangle is $60^\circ$. So, within this triangle, there are three circular sectors, each with an angle of $60^\circ$ and radius $r=2$. The total area of these three sectors is $3 \times \left(\frac{60}{360}\pi r^2\right) = 3 \times \left(\frac{1}{6}\pi (2^2)\right) = 3 \times \frac{4\pi}{6} = 2\pi$.
5. Calculate the shaded area: The shaded area is the area of the equilateral triangle formed by the centers minus the area of the three circular sectors within it. Shaded Area = Area$_{\text{triangle}} - \text{Area}_{\text{sectors}} = 4\sqrt{3} - 2\pi$.

This matches option (A).

The initial interpretation of the shaded area as the area of the large enclosing triangle minus the three circles leads to a result not among the options. Given the options and the commonality of this type of geometry problem, the shaded region refers to the area enclosed by the three circles.