Question

A rod of fixed length k has its ends sliding along the coordinate axes in $I^{st}$ quadrant such that rod meets the x-axis at A(a, 0) and y-axis at B(0, b). If O is origin and $E = \left(a + \frac{1}{b}\right)^2 + \left(b + \frac{1}{a}\right)^2$.

Which of the following holds good?

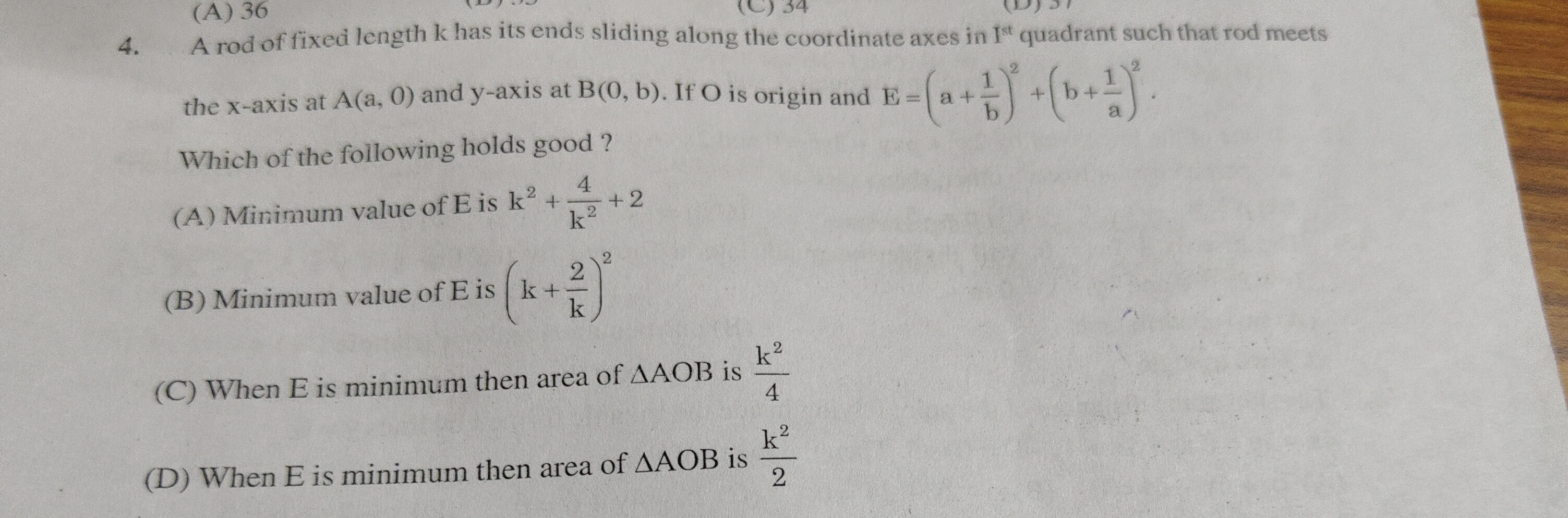
• A. Minimum value of E is $k^2 + \frac{4}{k^2} + 2$
• B. Minimum value of E is $\left(k + \frac{2}{k}\right)^2$
• C. When E is minimum then area of $\triangle AOB$ is $\frac{k^2}{4}$
• D. When E is minimum then area of $\triangle AOB$ is $\frac{k^2}{2}$

Answer 1

Answer: (B), (C)

B, C

Answer 2

The problem describes a rod of fixed length $k$ with its ends sliding along the coordinate axes in the first quadrant. Let the ends be $A(a, 0)$ on the x-axis and $B(0, b)$ on the y-axis. Since the rod is in the first quadrant, $a > 0$ and $b > 0$. The origin is $O(0,0)$.

1. Relation between a, b, and k: The length of the rod $AB$ is $k$. Using the distance formula or Pythagorean theorem for $\triangle AOB$: $OA^2 + OB^2 = AB^2$ $a^2 + b^2 = k^2$

2. Simplify the expression E: The expression given is $E = \left(a + \frac{1}{b}\right)^2 + \left(b + \frac{1}{a}\right)^2$. Expand the squares: $E = \left(a^2 + \frac{1}{b^2} + \frac{2a}{b}\right) + \left(b^2 + \frac{1}{a^2} + \frac{2b}{a}\right)$ Group terms: $E = (a^2 + b^2) + \left(\frac{1}{a^2} + \frac{1}{b^2}\right) + 2\left(\frac{a}{b} + \frac{b}{a}\right)$ Substitute $a^2 + b^2 = k^2$: $E = k^2 + \frac{k^2}{a^2 b^2} + \frac{2k^2}{ab}$ Factor out $k^2$: $E = k^2 \left(1 + \frac{1}{a^2 b^2} + \frac{2}{ab}\right)$ The term in the parenthesis is a perfect square: $E = k^2 \left(1 + \frac{1}{ab}\right)^2$

3. Minimize E: To minimize $E = k^2 \left(1 + \frac{1}{ab}\right)^2$, we need to minimize the term $\left(1 + \frac{1}{ab}\right)^2$. Since $a, b > 0$, $1 + \frac{1}{ab}$ is positive. Therefore, minimizing the square is equivalent to minimizing $1 + \frac{1}{ab}$. This occurs when the term $\frac{1}{ab}$ is minimized, which means the product $ab$ must be maximized.

4. Maximize ab: We need to maximize $ab$ subject to the constraint $a^2 + b^2 = k^2$ for $a, b > 0$. Using the AM-GM inequality: For positive numbers $a^2$ and $b^2$, $\frac{a^2 + b^2}{2} \ge \sqrt{a^2 b^2}$ $\frac{k^2}{2} \ge ab$ The maximum value of $ab$ is $\frac{k^2}{2}$. This maximum occurs when $a^2 = b^2$, which implies $a=b$ (since $a,b>0$). If $a=b$, then $a^2 + a^2 = k^2 \Rightarrow 2a^2 = k^2 \Rightarrow a^2 = \frac{k^2}{2}$. So, $a = b = \frac{k}{\sqrt{2}}$.

5. Calculate the minimum value of E: Substitute the maximum value of $ab = \frac{k^2}{2}$ into the simplified expression for E: $E_{min} = k^2 \left(1 + \frac{1}{\frac{k^2}{2}}\right)^2$ $E_{min} = k^2 \left(1 + \frac{2}{k^2}\right)^2$ $E_{min} = k^2 \frac{(k^2 + 2)^2}{k^4}$ $E_{min} = \frac{(k^2 + 2)^2}{k^2}$ $E_{min} = \frac{k^4 + 4k^2 + 4}{k^2}$ $E_{min} = k^2 + 4 + \frac{4}{k^2}$

   Now let's check the given options for the minimum value of E: (A) Minimum value of E is $k^2 + \frac{4}{k^2} + 2$. This is incorrect. (B) Minimum value of E is $\left(k + \frac{2}{k}\right)^2$. Expand $\left(k + \frac{2}{k}\right)^2 = k^2 + 2(k)\left(\frac{2}{k}\right) + \left(\frac{2}{k}\right)^2 = k^2 + 4 + \frac{4}{k^2}$. This matches our calculated $E_{min}$. So, option (B) is correct.

6. Calculate the area of $\triangle AOB$ when E is minimum: The area of $\triangle AOB$ is given by $\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times OA \times OB = \frac{1}{2} ab$. When E is minimum, $ab$ is at its maximum value, which is $\frac{k^2}{2}$. Area of $\triangle AOB = \frac{1}{2} \left(\frac{k^2}{2}\right) = \frac{k^2}{4}$.

   Now let's check the given options for the area of $\triangle AOB$: (C) When E is minimum then area of $\triangle AOB$ is $\frac{k^2}{4}$. This is correct. (D) When E is minimum then area of $\triangle AOB$ is $\frac{k^2}{2}$. This is incorrect.

Both options (B) and (C) hold good.