Question

A ring of radius $R$ having charge $Q$ is fixed in a horizontal plane. A point mass $m$ is at stable equilibrium at a distance $d$ from centre of ring as shown. If the charge on point mass is $q$, then

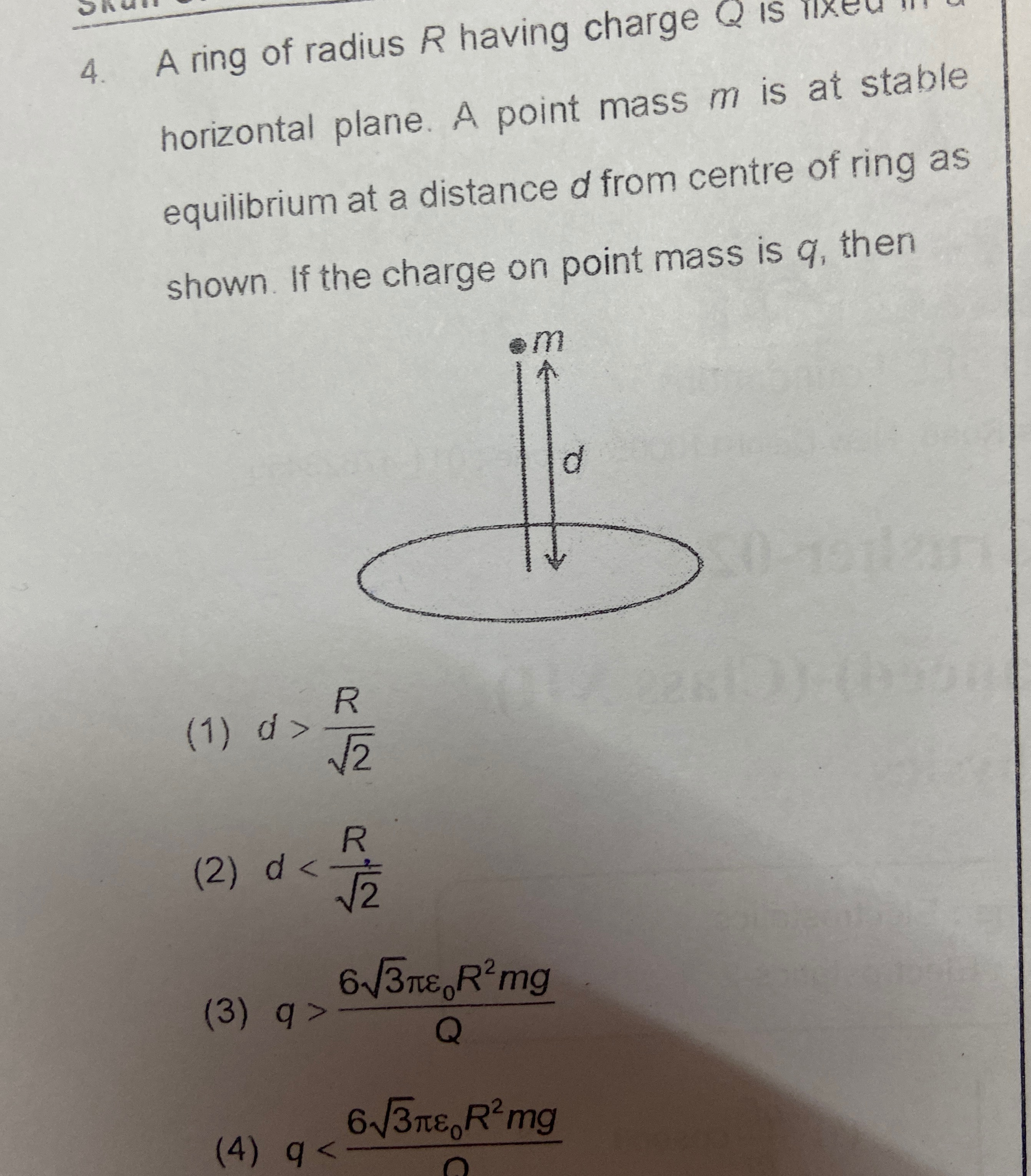
• A. $d > \frac{R}{\sqrt{2}}$
• B. $d < \frac{R}{\sqrt{2}}$
• C. $q > \frac{6\sqrt{3}\pi\epsilon_0 R^2 mg}{Q}$
• D. $q < \frac{6\sqrt{3}\pi\epsilon_0 R^2 mg}{Q}$

Answer 1

Answer: (B), (C)

The correct options are (2) and (3).

Answer 2

1. For a ring, the axial electric field is $E=\frac{Qd}{4\pi\epsilon_0(d^2+R^2)^{3/2}}$.

2. Equilibrium requires $qE=mg$ and stability demands $\frac{d^2U}{dz^2}>0$ which results in $d < \frac{R}{\sqrt2}$.

3. The function $q=\frac{4\pi\epsilon_0mg(d^2+R^2)^{3/2}}{Qd}$ is minimized at $d=\frac{R}{\sqrt2}$ giving $q_{\min}=\frac{6\sqrt3\pi\epsilon_0R^2mg}{Q}$. Thus, $q$ must exceed this value.