Question
Question: A current in circuit is given by i = 3 + 4 sin ωt. Then the effective value of current is :...
A current in circuit is given by i = 3 + 4 sin ωt.
Then the effective value of current is :
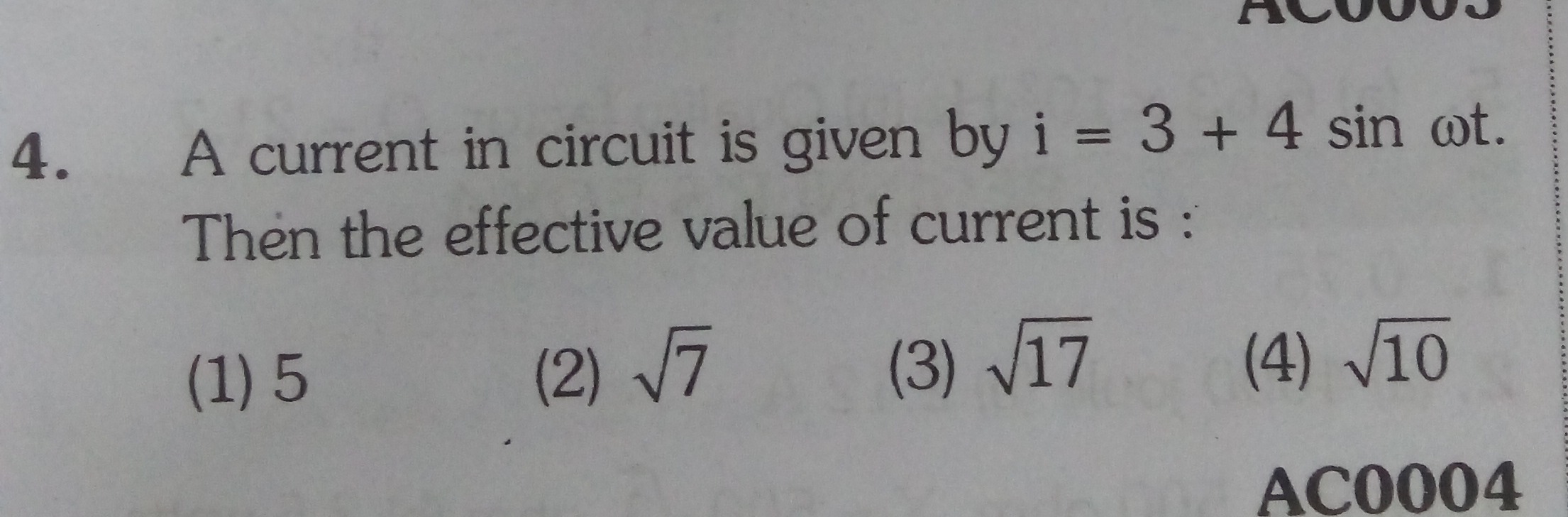
5
7
17
10
The effective value of the current is 17 A.
Solution
The current in the circuit is given by the equation:
i=3+4sinωt
This current consists of two components:
- A DC component (IDC)
- An AC component (IAC)
From the given equation:
The DC component, IDC=3 A. The AC component is IAC=4sinωt. This is a sinusoidal current with a peak value (amplitude) Im=4 A.
The effective value (or RMS value) of a current waveform containing both DC and AC components is given by the formula:
Ieff=IDC2+Irms(AC)2
First, we need to find the RMS value of the AC component. For a sinusoidal current with peak value Im, its RMS value is:
Irms(AC)=2Im
Substituting Im=4 A:
Irms(AC)=24 A
Now, substitute the values of IDC and Irms(AC) into the formula for the effective current:
Ieff=(3)2+(24)2
Ieff=9+216
Ieff=9+8
Ieff=17 A
Thus, the effective value of the current is 17 A.
